tarcza 1

ĆWICZENIE 5

ANALIZA PŁASKIEGO STANU NAPRĘŻEŃ - TARCZA

(TENSOMETRIA OPOROWA)

1 CEL ĆWICZENIA

Celem ćwiczenia jest zapoznanie się z. pracą tarcz w zakresie sprężystym Można przy tym dokonać rozwiązania następujących zadań:

a)    wyznaczyć eksperymentalnie rozkład naprężeń cr_y w przekroju AB i porównać go z rozkładem analitycznym wg wykładu WM [1],

b)    obliczyć współczynnik koncentracji naprężeń i porównać go z danymi z literatury np.

[3],

c)    oszacować wpływ nierównomierności obciążenia brzegów tarczy na rozkład naprężeń w środku jej obrysu,

%

2.    WYKONANIE ĆWICZENIA

Ad a) W przekroju z karbami AB należy wyznaczyć rozkłady odkształceń i naprężeń £_x,£_y,a_xr<7_y, jako funkcje x. Z punktu

widzenia WM jest to przypadek rozciągania pręta z osłabionym przekrojem. W myśl zaleceń WM wzory jej nie powinny być stosowane w tym obszarze. Niemniej oszacowanie wykonane dla przekroju osłabionego da wartość:

P P

cj — ——- = — = const A_ab Sh

(nie zależy od współczynnika x),    (1)

cr_v = 0.

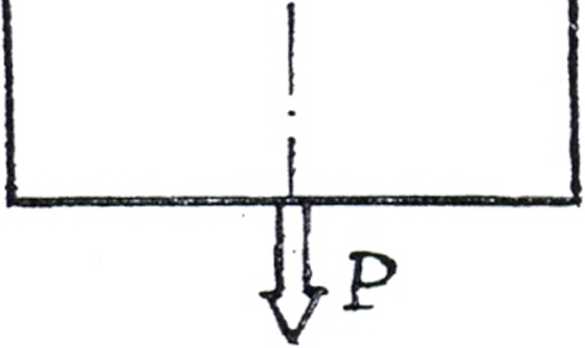
Rys. 1

1