str025 (5)

5 3. FUNKCJE ZESPOLONE ZMIENNEJ ZESPOLONEJ 25

Po wprowadzeniu następujących oznaczeń

Im 1 = p, I = a + ip.

Re / = a,

możemy napisać

(2)

z = ix.

Wyznaczamy obecnie w jaką linię w płaszczyźnie (a, P) przekształca funkcja (1) prostą Rez = 0. Równanie tej prostej możemy zapisać w postaci (3)

Uwzględniając (2) i (3) w funkcji (1), otrzymujemy związek

U

a+iP =

R + ix

a stąd mamy parametryczne równania przekształconej linii (3) w płaszczyźnie (a,/?)

UR

a = ■

(4)

/*=-

R² + x² * Ux

R²+x² '

gdzie xe (— ao, oo).

Po wyrugowaniu parametru x z równań (4) otrzymujemy równanie okręgu

(5)

1 „2 U

a ² + p² =— a. R

Z tego, że i?> 0 wynika, że odwzorowana linia jest okręgiem (5).

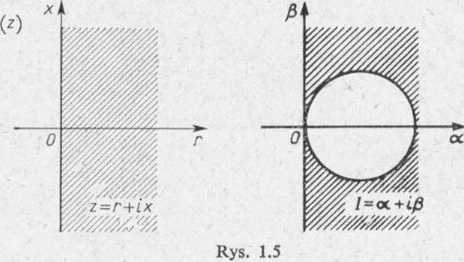
Na rysunku 1.5 przedstawiony jest obszar zmienności impedancji z na płaszczyźnie (r, x) oraz odwzorowany przez funkcję (1) obszar zmienności natężenia prądu / w płaszczyźnie (a, P). Zakreskowane powierzchnie na rysunku 1.5 przedstawiają wyżej wymienione obszary.

Zadania do rozwiązania

1. Określić pole funkcji oraz jej część rzeczywistą i urojoną:

a) w = z⁴, b) w =

z+1

z^T’

c) w =

1

1 —z

2 ■