str053 (5)

§ 8. WZÓR CAŁKOWY CAUCHY'EGO I JEGO UOGÓLNIENIE 53

§ 8. WZÓR CAŁKOWY CAUCHY'EGO I JEGO UOGÓLNIENIE 53

ystać wartości całki Poissona,

>Q

$exp( — )exp(-uR ).

yi bi)	1 ^JJ C(R+bi)
	i
0	J, B(R) x

Rys. 1.12

jeżeli zaś funkcja f(x) zmiennej rzeczywistej ma pierwszą pochodną w pewnym przedziale, to nie tylko może nie mieć drugiej pochodnej, ale nawet pierw-sza pochodna może być nieciągła. Wzór (8.2) nosi nazwę uogólnionego wzoru całkowego Cauchy’ego. Otrzymujemy go przez n-krotne zróżniczkowanie wzoru (8.1) względem parametru z.

Zadania przykładowe

f—---dz,

J z(z-2i)

Zadanie 8.1. Obliczyć całkę

(1)

gdzie C oznacza okrąg skierowany dodatnio o promieniu 2i oraz środku 3i. Rozwiązanie. Zauważmy, że

gdzie

(2)

dzcnie całkowe Cauchy’ego, nr całkowania C, jak następuje

r_£-*- fM*.

J 2(2-2i) J 2-2.

/(*)—•

Z

lie

bszarze jednospójnym domknię-wewnętrznym z obszaru D wy-

D.

Orzeka on, że wartości /(£) inkcji w każdym punkcie wetów). Jeżeli funkcja f{z) jest irego brzegiem jest kontur C, e wszystkich rzędów. Pochodne

i

,2,...

:nia w sposób istotny funkcje ilnych zmiennej rzeczywistej, anej zespolonej ma pochodną ockodne wszystkich rzędów,

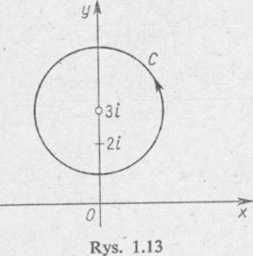
Funkcja (2) jest holomorficzna wewnątrz i na konturze C (rys. 1.13). Wobec tego zgodnie ze wzorem (8.1) zastosowanym do funkcji (2) w punkcie z = 2i, mamy

A,

e^21 1	r/(o
2i 2ni J	k-2 i
c
e^2‘ 1 i	( ^ei
2 i 2 u i J	k(f-

2ni-

,e²ⁱ f

¹¹2i Ję(C-

c

n (cos 2+i sin 2) = j*

20

,{

dC,

C(C-20

rA-