str123 (5)

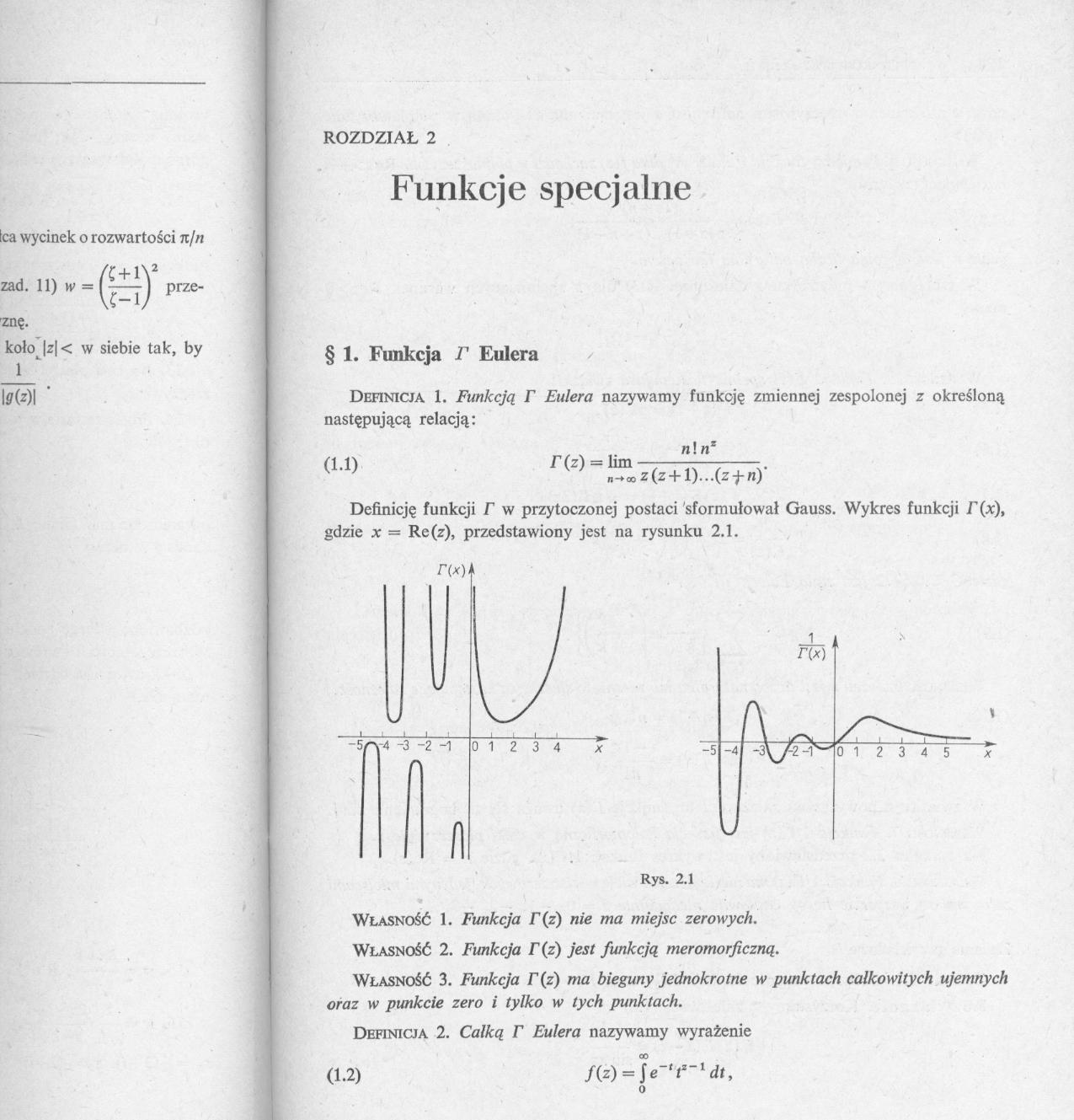
o rozwartości n/n

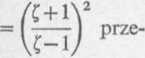
w siebie tak, by

ROZDZIAŁ 2

Funkcje specjalne

§ 1. Funkcja r Eulera

Definicja 1. Funkcją r Eulera nazywamy funkcję zmiennej zespolonej z określoną następującą relacją:

(U)

T(z) — lim —

n-+ oo Z

n\n^z

(z+l

Definicję funkcji F w przytoczonej postaci sformułował Gauss. Wykres funkcji r(x), gdzie x = Re (z), przedstawiony jest na rysunku 2.1.

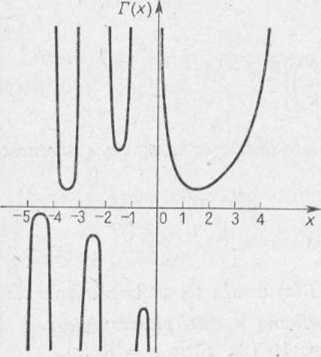
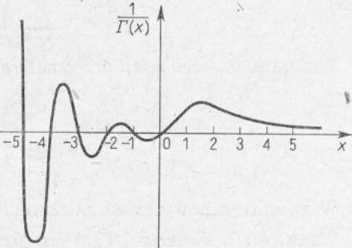
Rys. 2.1

Własność 1. Funkcja f(z) nie ma miejsc zerowych.

Własność 2. Funkcja T(z) jest funkcją meromorficzną.

Własność 3. Funkcja r(z) ma bieguny jednokrotne w punktach całkowitych ujemnych oraz w punkcie zero i tylko w tych punktach.

Definicja 2. Całką F Eulera nazywamy wyrażenie

(1.2)    /(z)=Je-^,F-¹dt,

0