Image72 (9)

142

3.10. Zdarzenie A może być przyczyną zdarzeń C i D, natomiast zdarzenia C i D nie mogą być przyczyną żadnego z pozostałych zdarzeń.

3.11. Na diagramie Minkowskiego przedstawiamy linię świata stacji

kosmicznej oraz linię odpowiadającą komunikatowi z planety (rys.52).

Równania linii są następujące:

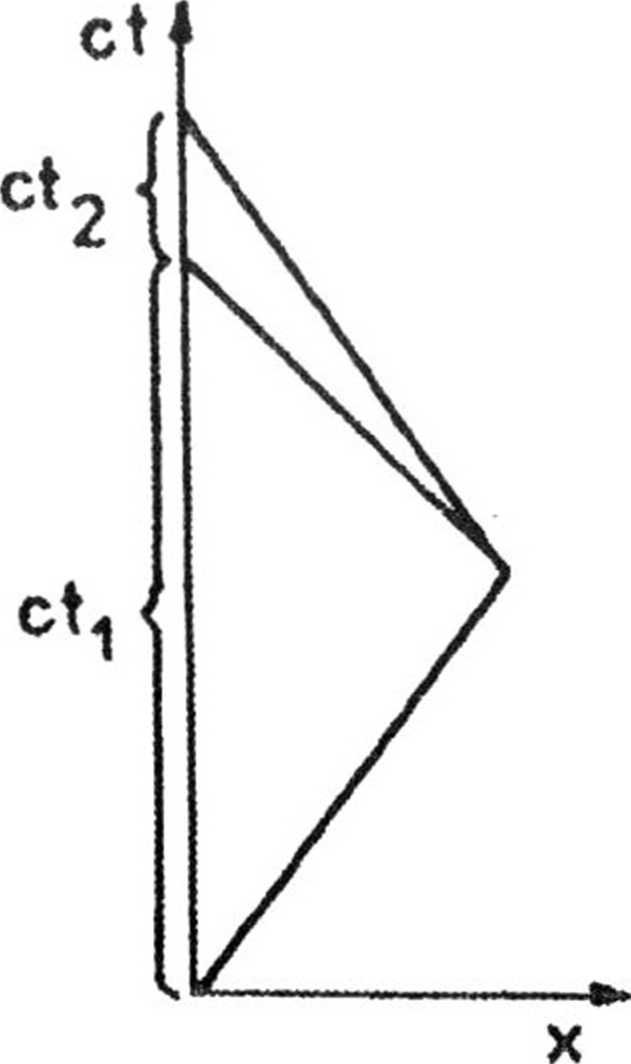
Rys.52

Ct = - X V

ct = —

- pierwszy etap podróży,

- x -f c (£, + t₂) - drugi etap podróży,

v

ct — —x 4- ct

- komunikat z planety,

gdzie:    - czas, jaki upłynął od chwili startu do mo

mentu otrzymania komunikatu z planety, t₂ - czas, jaki upłynął od tego komunikatu do chwili powrotu stacji na Ziemię. Eliminując z tych równań x, otrzymujemy po przekształceniach

t

1

v = c

t

t

A 1

Z treści zadania wynika, że — = k = 3. Stąd poszukiwana prędkość rakiety

ti

1

v =

2 ^C

3.12

a. Czas życia cząstki w układzie laboratorium wynosi 2,29 [/xs].

czasie jest rzędu

b. Średnia droga, jaką przebyła cząstka w tyi 6,18 • 10² [m].

c. W tym przypadku przebyta droga jest rzędu 2,7 • 10² [m]

3.13. Czas t' mierzony na pokładzie satelity wiąże się z czasem ziemskim t równaniem

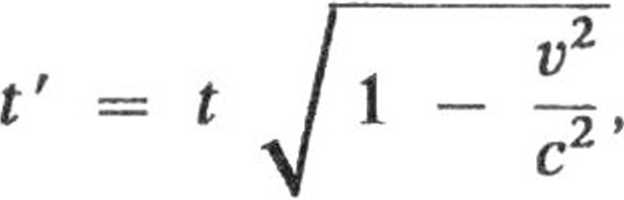
gdzie prędkość satelity v c.

w szereg (ograniczony do wyrazów

II

Zastępując pierwiastek jego rozwinięcie kwadratowych) i podstawiając

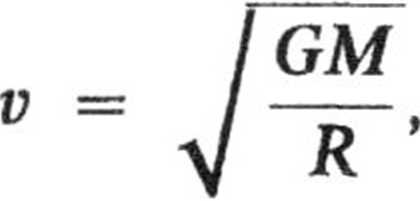
mamy

£'

t 1 -

GM

2 Rc²

Przekształcając to równanie otrzymujemy

t

2 Rc GM

(1-0 = 3- 10⁹ [s]

3.14.    1 [m].

3.15.    5,28 ff 6 /.

3.16. L = L

1

V

j cos^z(p — 0,8 L

3.17. Oznaczając przez L' długość pręta w układzie U\ mamy

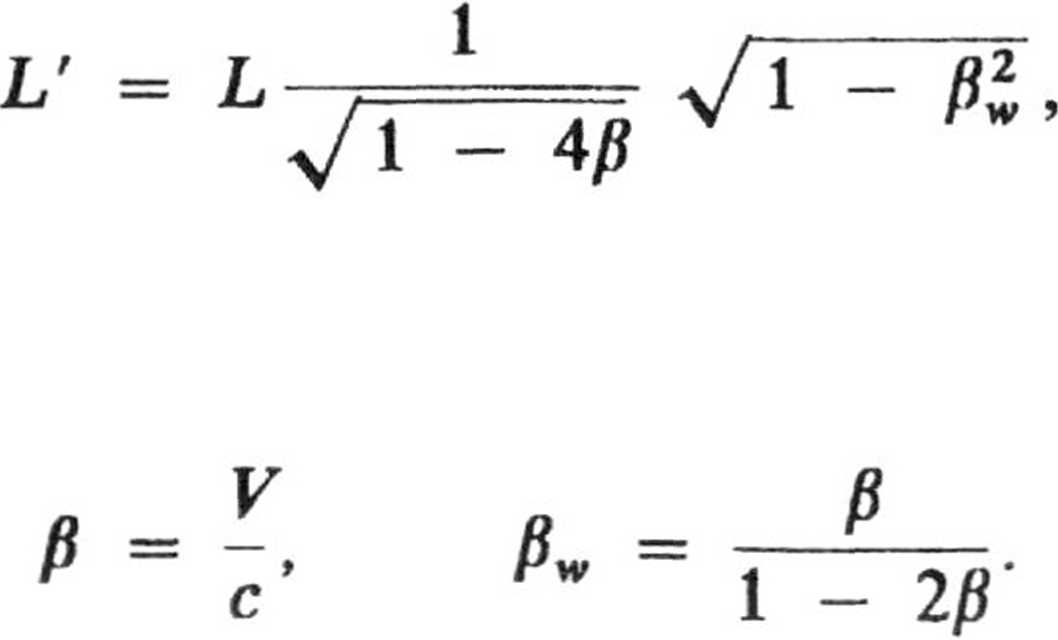
gdzie: