img156

Inną, często używaną miarą rozproszenia jest wariancja skorygowana o], którą definiujemy jako:

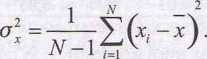
(6.12)

Wielkości przedstawione równaniami (6.11) i (6.12) służą do oceny niepewności pojedynczego pomiaru.

Ważnym zagadnieniem w teorii błędów jest analiza rozkładu średnich arytmetycznych z kilku serii pomiarów przeprowadzonych w takich samych warunkach. Każda z otrzymanych średnich będąc najlepszym przybliżeniem wartości prawdziwej X przyjęłaby jednak inną wartość. Przeprowadzone analizy dowiodły, że rozrzut średnich z wielu serii pomiarów opisać można znanym już rozkładem normalnym skupionym wokół wartości prawdziwej X. W tym przypadku miarą rozproszenia jest odchylenie standardowe średniej arytmetycznej dane równaniem:

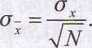
(6.13)

Parametr zdefiniowany równaniem (6.13) niesie więc informację o wielkości możliwego błędu średniej arytmetycznej obliczonej z Npomiarów w stosunku do wartości prawdziwej ^populacji generalnej. Łatwo zauważyć, że zmniejszenie błędu średniej arytmetycznej jako najlepszego przybliżenia wartości prawdziwej związane jest ze wzrostem liczby pomiarów.

Odchylenie standardowe określone wzorem (6.11) wykorzystywane jest często do definiowania przedziału wartości granicznych w równaniu (6.9). Najczęściej poszukujemy prawdopodobieństwa, że wynik kolejnego pomiaru znajdzie się wewnątrz przedziału o promieniu e_g= ta wokół wartości prawdziwej X. W tym przypadku t oznacza dowolną liczbę dodatnią. Po przyjęciu powyższych założeń równanie (6.9) przyjmuje postać:

^    A +r(7

P(X-to<x<X + to) = —y= f e-^tx-^xfn°’dx.    (6.14)

od2n x-ta

Ponieważ obliczanie całki opisanej równaniem (6.14) dla różnych przedziałów wartości granicznych jest pracochłonne, najczęściej korzystamy z gotowych wyników, które w naszym przypadku zamieszczono w formie tablicy 6.1. Nietrudno zauważyć, że prawdopodobieństwo uzyskania pojedynczego wyniku w promieniu jednego odchylenia standardowego <r od wartości prawdziwej Xwynosi 68,27%. Dla promienia 2a analizowane prawdopodobieństwo wynosi już 95,45%, a w promieniu 3<7- 99,73%. Wynika stąd, że uzyskanie wyniku odbiegającego od wartości prawdziwej Xo więcej niż 3cr w przypadku wielokrotnych pomiarów tej samej wielkości jest bardzo mało prawdopodobne.