img314 (6)

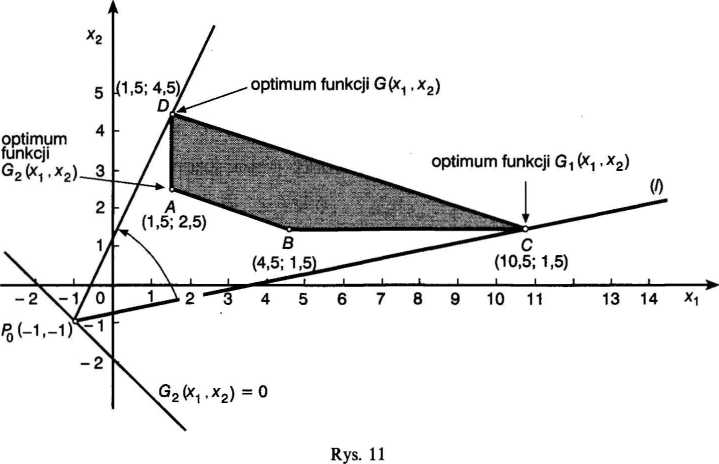
Obracając prostą rozwiązującą wokół punktu P₀(—1, —1), otrzymujemy jej skrajne położenia, tzn. punkty D i C. Wartości funkcji G(x₁,x₂) w tych punktach wynoszą:

G( 1,5; 4,5) = y = 3    G(10,5; 1,5) = ^ = 2 A

Ponieważ C?(1,5; 4,5) > G (10,5; 1,5), przeto funkcja G(x_1;x₂) osiąga maksimum w punkcie Z), a więc *i = 1,5 i jc₂ = 4,5. Minimum zaś funkcja G(x₁,x₂) osiąga w punkcie C, a więc dla x\ = 10,5 i x'₂ = 1,5.

Zauważmy, że kolejne rozwiązania z pkt. 1-3 różnią się między sobą. Jest rzeczą oczywistą, że inną wartość liczbową przyjmuje rozwiązanie dla funkcji celu G₁(x_l,x₂) maksymalizowanej (punkt C), inną zaś dla funkcji celu G₂(x_vx₂) minimalizowanej (punkt A). Jeszcze inne, trzecie kolejne rozwiązanie jest kompromisem przy zadaniu jednoczesnej realizacji dwóch kryteriów: G₁ i G₂ Optimum w tym przypadku stanowią współrzędne punktu D, a więc x\ = 1,5 i x₂ = 4,5.

Pytania i problemy

1.    Wskazać zasadniczy cel, w jakim korzysta się z modelu programowania ilorazowego.

2.    Omówić różnice w konstrukcji między dotychczas poznanymi modelami programowania liniowego a nowo przedstawionym modelem PI.

3.    Wymyślić i opisać kilka przykładów sytuacji mogących zaistnieć w praktyce gospodarczej, w których może znaleźć zastosowanie poznana konstrukcja modelowa.

4.    W pewnym zadaniu PI funkcja celu przybiera postać:

Gd*) x,+ x₂ + 2

_ , . = ------- max.

G₂(x)    12x, + 3x₂ + 15

	G2(x) 12.*,+3*2+15 ----► min (jl(.x) + X2~ł~2
a)    spowoduje zmianę współrzędnych punktu P0 (xj, x‘), b)    może wywołać zmianę rozwiązania optymalnego. 5. Dany jest następujący czworobok, który stanowi zbiór rozwiązań dopuszczalnych: .4(2; 2), B(5; 1), C(4; 4), D{ 1; 5) oraz punkt P0(— 1;— 1). W których punktach spośród czterech podanych możliwe jest rozwiązanie optymalne?
	Zadania
52. Rozwiązać stosując metodę geometryczną następujący program:
(1)	xx + 2x2^8 ,
(2)	xt + x2^8,
(3)	— Xj + x2<l,
(4)	xt — 2x2 ^4,
(5)	0^*2 <6,
(6)
(7)	—x,+x2 — 8 ^F(X‘’^X‘^> = *i + *2 + 4
53. Dany jest program liniowy z funkcją celu w postaci ułamkowej:
(1)	x1+x2^ 6,
(2)	— x1+x2sś; 3,
(3)	2x1 + x2^12,
(4)	x15x2^2,
(5)	, , x, — 2x2 + 2 H(x.,x2) = -T^1--—7 -*■ max. ^v 1v 3xj — x2 + 6
1.    Rozwiązać zadanie stosując metodę geometryczną. 2.    Podać wartość funkcji celu dla optimum.
54. Dane jest zadanie PI:
(1)	xt—x2^0,
(2)	2xj +x2^6,
(3)	xx + x2<6,
(4)	x1+x2^5,

85