img433 (2)

«

wynika, że wtedy wartości funkcji J'(x) dodatnie, zatem mamy

5

t

- (x - 1) (x + 1) dążą do zera, ale są

lim

x-»T

x + 4

[-(x-1)(x + 1)]

= +00.

Natomiast

I

o⁺

5

t

lim,

x->1 ⁺

x + 4

h(x-1)(x+ 1)]

V___j

— —00.

o-

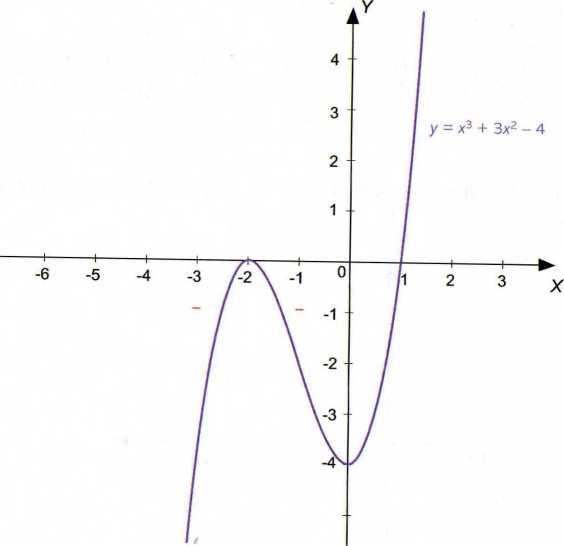
Ad c) Stwierdzamy bez trudu, że jeśli x-» -2~, to licznik ułamka dąży do -6, mianownik zaś do O. Szkicujemy wykres funkcji /(x) = x³ + 3x² - 4 (z mianownika), zauważając wcześniej, że x³ + 3x² - 4 = (x + 2)²(x - 1):

Utrzymujemy więc

x² + 5x

Hm “9-r-5--

« > - x³ + 3x² - 4

T

.. x² + 5x

= +qo oraz lim , —----

*->-2⁺ x³ + 3x² - 4

= +oo.

~v—

4

o-

4

0-

PlfYKIAD 13.

W lenili względności, stworzonej przez Einsteina, wykorzystuje się wzory:

i = L(v) = Zh

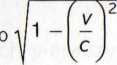
oraz m = m(v) =

m₀

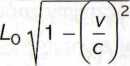
heiw./y z nich wyraża zależność długości L obiektu poruszającego się względem obserwatora od prędkości v tego obiektu, przy czym L₀ jest długością tego obiektu w stanie spoczynku. Drugi wzór wyraża zależność masy m obiektu |»oiu*,/ającego się z prędkością v od tej prędkości, przy czym m₀ to masa tego nblnklu w stanie spoczynku. W obu wzorach c oznacza prędkość światła. Znajdziemy i zinterpretujemy lim\ L(v) oraz lim_m(v). Dlaczego musimy tu użyć gra-

V—>C    V—>C s

nic Jednostronnych? Mamy lim L(v) = lim

!/-»C    V->C

m₀

Urn m(v) = lim

V H    V-»C

1-

V^C?

= + 00.

1 -

V^C7

- 0 oraz

4

o⁺

/ | ilerwszego wzoru wynika, że wraz ze wzrostem prędkości v rośnie wartość ułamka V

’N2~

tym samym maleje liczba

, a więc maleje także długość L. Obliczo

na zaś granica mówi nam, że im bliższa prędkości światła jest prędkość obiek-tu, tym bliższa zera okazuje się długość tego obiektu dla obserwatora.

Drugi wzór pokazuje, że wraz ze wzrostem prędkości v rośnie wartość ułamka

, tym samym maleje liczba J1 -

V^C?

, a więc rośnie liczba

1

czyli rośnie też masa m. Druga granica mówi o tym, że im bliższa prędkości