10 (40)

191

Twierdzenie o funkcji uwikłanej

i z (57) wynika, że f(#(y)) = 0 w W. Reguła różniczkowania funkcji złożonej pokazuje wtedy, że

f'(#(y))4>'(y) = 0.

Jeżeli y = b, to <P(y) = (a, b) i f'(#(y)) = A. Wobec tego

(64)    A4>'( b) = 0.

Z (64), (63) i (54) wynika więc, że dla dowolnego keR"

A*g'(b)k+A,k = A(g'(b)k, k) = A4>'(b)k = 0.

Zatem

(65)    ^xg'(b)+A_y = 0,

która to równość jest równoważna z (58). To kończy dowód.

Uwńga. Wzór (65) wyrażony w terminach składowych funkcji f i g przyjmuje postać

i (Djfi) (a, b) (D_kgj) (b) = ~(D_n+kf_t) (a, b) j=i lub

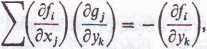
Ff

gdzie 1 < i < n, 1 < k < m.

Dla każdego k jest to układ n równań liniowych, w których niewiadomymi są pochodne dgj/fy_k (1 < j < h),

9.29. Przykład. Niech n = 2, m = 3. Rozważmy odwzorowanie f — (f_uf₂) z R⁵ do R² dane za pomocą funkcji

x₂,||y₂,y₃) « 2e^xL+x₂y_l-4y₂+3, f2(x_u x₂, y_lt y₂,y₃) = x₂cosx,-6x_l+2>-₁-y₃.

Dla a = (0,1), b = (3,2,7) mamy f(a, b) = 0.

Przekształcenie liniowe A = f'(a, b) ma względem baz standardowych macierz

f 2 3 1 -4    0]

¹ ] L-« i 2 0 -lj

Zatem

Widzimy stąd, że wektory kolumnowe macierzy [AJ są liniowo niezależne. Zatem A_x jest odwracalna, i twierdzenie o funkcjach uwikłanych gwarantuje istnienie odwzorowania g