IMGç88 (2)

pomiaru czasu i cz─Östotliwo┼Ťci. Gdy bowiem bramka otwarta jest na czas mierzony (7', lub t, rys 2.3 a), w├│wczas zliczane s─ů impulsy sygna┼éu zegarowego (z generatora o cz─Östotliwo┼Ťci wzorcowej /ÔÇ×), a wynik zliczenia jest w przybli┼╝eniu liczb─ů okres├│w (T.) sygna┼éu zegarowego (sygna┼éu tzw podstawy czasu), kt├│re zmie┼Ťci┼éy si─Ö w mierzonym czasie T, lub Inaczej mo┼╝na powiedzie─ç, ┼╝e liczba impuls├│w wyra┼╝a w zaokr─ůgleniu krotno┼Ť─ç wielko┼Ťci T, w stosunku do wielko┼Ťci Tw, a wi─Öc zgodnie z istot─ů pomiaru jest wynikiem mierzenia T,. Gdy natomiast bramka otwarta jest na czas wzorcowy Tw (rys. 2.3b), w├│wczas zliczane s─ů impulsy o cz─Östotliwo┼Ťci fÔÇ× powsta┼ée z sygna┼éu badanego, a liczba zliczonych impuls├│w wyra┼╝a w zaokr─ůgleniu liczb─Ö okres├│w Tx sygna┼éu o cz─Östotliwo┼Ťci /ÔÇ× kt├│re zmie┼Ťci┼éy si─Ö w czasie wzorcowym 7┬╗, taka liczba wyra┼╝a zgodnie z definicj─ů cz─Östotliwo┼Ť─ç.
|
W0 |
Ti |
w.. |
-1*-v. | |
|
Ôľá |
r-ÔÇ× |
F |
"1 | |
|
V |
Iw | |||
|
U(0 |
Jw~'/fw |
U─ä | ||
|
mu |
muf |
iiiiiiiiiiiiiiiiumii 1 |
lin |
iiiiiiiiiiiiiiiiiiiiii |
|
J nT, 1 tw |
i_aL_J S | |||
|
a |
b | |||
Rys. 2. 3. Przebiegi napi─Ö─ç na wej┼Ťciach s i p bramki: a - przy pomiarze czasu T,\ b - przy pomiarze cz─Östotliwo┼Ťci f w czasie wzorcowym T.
Stan ko┼äcowy zliczania jest przepisywany z licznika do rejestru (pami─Öci) i tam podtrzymywany do momentu, kiedy b─Ödzie wpisywany nast─Öpny wynik zliczania. Stan rejestru jest nast─Öpnie dekodowany na uk┼éad napi─Ö─ç potrzebny do wysterowania wy┼Ťwietlacza lub na kod odpowiedni do przes┼éania wyniku do innych system├│w cyfrowych. Wy┼Ťwietlenie danej jednostki i przecinka dziesi─Ötnego na wy┼Ťwietlaczu jest dobierane odpowiednio do wybranej funkcji pomiarowej i zaczepu dzielnika (podzakresu)
2.3.2. Analiza procesu kwantowania
Przeprowadzimy analiz─Ö procesu mierzenia czasu i cz─Östotliwo┼Ťci realizuj─ůcego si─Ö w uk┼éadzie bramka-licznik ze wzgl─Ödu na to, ┼╝e otwarcie bramki i pierwszy zliczany impuls nie musz─ů wyst─ůpi─ç r├│wnocze┼Ťnie, nie musi mie─ç miejsce synchronizacja. R├│wnie┼╝ moment zamkni─Öcia czasu zliczania me musi zbiec si─Ö z ostatnim impulsem zliczanym, bo mierzony czas T, nie musi by─ç ca┼ékowit─ů wielokrotno┼Ťci─ů okresu zliczanych impuls├│w. Ten ostatni fakt, wyra┼╝aj─ůcy si─Ö tym, ┼╝e stan wielko┼Ťci (w naszym przypadku np. odst─Öp czasu) wyra┼╝amy za pomoc─ů ca┼ékowitej krotno┼Ťci innego stanu wielko┼Ťci tego samego rodzaju (w og├│lnym przypadku w zaokr─ůgleniu), nazywa si─Ö w miernictwie procesem kwantowania (dyskretyzacji). U┼╝ywaj─ůc wprowadzonego terminu powiemy, ┼╝e b─Ödziemy analizowa─ç proces kwantowania czasu realizowany w cz─Östotliwo┼Ťciomierzu-czasomierzu cyfrowym, 1 Dzia┼éanie jest identyczne pod wzgl─Ödem istoty z tym, kt├│re podejmujemy, gdy przyk┼éadamy przymiar z podzialk─ů milimetrow─ů do przedmiotu, ┼╝eby zmierzy─ç jego d┼éugo┼Ť─ç
z─Öby okre┼Ťli─ç wp┼éyw tego procesu na dok┼éadno┼Ť─ç wskazania przyrz─ůdu (problem kwantowania cz─Östotliwo┼Ťci przy cyfrowym pomiarze cz─Östotliwo┼Ťci jest taki sam)
Na rys. 2.4 pokazano w powi─Ökszeniu fragmenty zakre┼Ťlone okr─Ögami na rys 2 Ja W ten spos├│b przedstawiono graficznie mo┼╝liwy, losowy uk┼éad chwil otwarcia bramki i wyst─ůpienia pierwszego impulsu zliczanego.
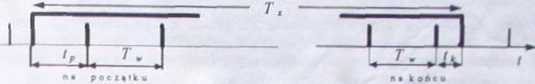
Rys. 2. 4. Przyk┼éadowy uk┼éad impuls├│w (w powi─Ökszeniu) na pocz─ůtku i na ko┼äcu otwarcia bramki na czas T. (powi─Ökszenie fragment├│w otoczonych okr─Ögami zakre┼Ťlonymi na rys 2 Ja)
Niech pierwszy zliczany impuls pojawi si─Ö po czasie r, < T. W├│wczas zaliczenie lego impulsu wywo┼éa wskazanie r├│wne jedynce, kt├│re b─Ödzie interpretowane jako jeden okres T. przebiegu o wzorcowej cz─Östotliwo┼Ťci,' gdy faktycznie zrealizowa┼é si─Ö kawa┼éek lego okresu na pocz─ůtku mierzonego czasu T, Na pocz─ůtku zliczania powsta┼éby wi─Öc b┼é─ůd wskazania A, * 7V-r, > 0: przyrz─ůd pokaza┼éby za du┼╝o. bo pokaza┼éby 17v, a powinien pokaza─ç kawa┼éek T, r├│wny lh czego ÔÇ×nie potrafi". Podobnie mog┼éaby powita─ç rozbie┼╝no┼Ť─ç na ko┼äcu mierzonego okresu TÔÇ×: zrealizowa┼éby si─Ö czas /i. zamkn─Ö┼éaby si─Ö bramka (bo sko┼äczy┼é si─Ö mierzony czas Tg), a na poczet tego czasu licznik zarejestrowa┼éby zero (impuls zamykaj─ůcy len zapocz─ůtkowany okres T. pojawia si─Ö po zamkni─Öciu bramki). Powsta┼éby b┼é─ůd wskazania na ko┼äcu mierzonego okresu czasu T.: At - 0-h = <0. Obserwator b─Ödzie odczytywa┼é wynik, kt├│remu odpowiada wypadkowy skutek rycb
zdarze┼ä. Z lego powodu powinni┼Ťmy zapyla─ç: jaki b─Ödzie udzia┼é sumy r,┬╗ r, (a w┼éa┼Ťciwie b┼é─Öd├│w A,*A) we wskazaniu przyrz─ůdu albo r├│wnowa┼╝nie zapyta─ç - jaki b─Ödzie b┼é─ůd wypadkowy wskazania z tego powodu.
Niech mierzony okres czasu T, b─Ödzie ca┼ékowit─ů wielokrotno┼Ťci─ů okresu wzorcowego Tm czyli T, - nT. (n liczba naturalna). Gdyby by┼éa synchronizacja i gdyby pierwszy impuls pojawiaj─ůcy si─Ö w chwili otwarcia bramki nie by┼é zliczany, a ostatni byl, to wskazanie przyrz─ůdu wynios┼éoby n i by┼éoby dok┼éadnym wskazaniem liczby okres├│w T. mieszcz─ůcych si─Ö w mierzonym czasie T,. Gdy nie ma jednak synchronizacji, ale T, jest nadal ca┼ékowit─ů wielokrotno┼Ťci─ů okresu TÔÇ× to T, - lr+(n-l)T.+it - nTÔÇ× bo /,+/┬╗- T. (wida─ç to z rys. 2.4). czyli b┼é─ůd wskazania - wynikaj─ůcy z kwantowania - te┼╝ r├│wna┼éby si─Ö zeru. Tak wi─Öc synchronizacja czy brak synchronizacji daje takie same wskazanie w przypadku, gdy T. - nT. Oznacza to. ┼╝e synchronizacja nic jest potrzebna.
Rozpatrzymy teraz przypadek bardziej typowy, gdy T. * nT. (nie ma takiego naturalnego n) Taki przypadek mo┼╝emy r├│wnowa┼╝nie zapisa─ç: T. - nT.+Al (dr jest nadwy┼╝k─ů - reszt─ů - zawart─ů w T. ponad ca┼ékowit─ů, najwi─Öksz─ů wielokrotno┼Ť─ç T. i jako reszta jest mniejsza od T.) Gdyby by┼éa synchronizacja i spe┼énione by┼éy przyj─Öte uprzednio warunki, lo czas AKT. nigdy me by┼éby uwzgl─Ödniony we wskazaniu przyrz─ůdu, a wskazania by┼éyby zawsze o dr mniejsze, czyli b┼é─ůd bezwzgl─Ödny wskazania przyrz─ůdu z tego powodu r├│wna┼éby si─Ö -dr i by┼éoby |-dr|<TÔÇ×. Przeci─Ötnie (┼Ťrednio dla wielu wskaza┼ä) mo┼╝na oczekiwa─ç b┼é─Ödu o warto┼Ťci ┼Ťredniej -0.57U bo ka┼╝dy czas trwania T, powinien by─ç jednakowo prawdopodobny Gdy jednak nic ma synchronizacji i r├│wnocze┼Ťnie ┼╝adna wielko┼Ť─ç T, me jest uprzywilejowana', a za┼éo┼╝enia poprzednio przyj─Öte s─ů takie same, lo b┼é─ůd wskazania b─Ödzie si─Ö losowo zmienia─ç w przedziale ┬▒T. o warto┼Ťci oczekiwanej r├│wnej zero i o tr├│jk─ůtnym rozk┼éadzie g─Östo┼Ťci prawdopodobie┼ästwa. B─Ödzie lak dlatego, te na ko┼äcu otwarcia bramki zrealizuje si─Ö czas r,*dr (ponad nT.), gdzie r, nie wprowadza b┼é─Ödu (by┼éo juz
1 Istot─ů sytuacji jest to, ┼╝e zliczane s─ů fizycznie impulsy, a powinny by─ç zliczane okresy W czasie T, mo┼╝e wyst─ůpi─ç impuls i zostanie zliczony, a odpowiadaj─ůcy mu okres T. zrealizuje si─Ö cho─çby w cz─Ö┼Ťci poza czasem T,.
1 Rozumiemy lo lak, ┼╝e wielko┼Ť─ç T, jest losowa i losowy jest wi─Öc odst─Öp czasu dr ponad najwi─Öksz─ů, ca┼ékowit─ů krotno┼Ť─ç nT. dla danego 7V Losowo┼Ť─ç liczby ca┼ékowitej n nas nie interesuje, tylko lej reszty dr Modelowanie rozk┼éadem jednostajnym (prostok─ůtnym) losowy rozrzut warto┼Ťci dr jest uzasadnione speku┼éa-tywnie i do┼Ťwiadczalnie. Natomiast b┼é─ůd kwantowania jest wynikiem dwu niazalc┼╝nych zdarze┼ä losowych: r, i Al.
61
Wyszukiwarka
Podobne podstrony:
Pomiar czasu i cz─Östotliwo┼Ťci: Okresem T sygna┼éu nazywamy czas jednej pe┼énej zmiany przebiegu sygna┼é
Pomiar czasu i cz─Östotliwo┼Ťci: Jednostk─ů okresu (czasu) jest sekunda (s), cz─Östotliwo┼Ťci herc (Hz).
Pomiar czasu cz─Östotliwo┼Ťci metod─ů oscyloskopow─ů:
SCAN0351 3. METODY OSCYLOSKOPOWE POMIARU CZASU I CZ─śSTOTLIWO┼ÜCI. 3.1. Metoda po┼Ťre
382300 Przyrz─ůdy do pomiaru czasu i cz─Östotliwo┼Ťci 382500 Przyrz─ůdy do pomiaru sk┼éadu i w┼éa┼Ťciwo┼Ťci
P1100153 Zasada pomiaru czasu St=tK- ts Sygnał satelitarny jest przesunięty względem sygnału generow
page0729 7*1Ssnogorz├│w ÔÇö Smognlecki czys┼éawa II, gdy Czesi Szl─ůsk pustoszyli, tu na czas niejaki z W
Wyst─ůpi ona wtedy, gdy: ÔÖŽ pracownik b─Ödzie prowadzi┼é na w┼éasny rachunek lub w cudz
Systemy tela Zadanie 1 Sygna┼é o cz─Östotliwo┼Ťci f= 900MHz i mocy P=6dBm podawany jest na wej┼Ťcie dopa
120(1) r Pole S,lABy}, w przypadku gdy ca┼éy trapez po┼éo┼╝ony jest na prawo od osi Oy, dane jest ca┼ék─ů
mechanika (2) Mechanika h p─ÖjlkiJ┼Ťj v p funkcji czasu t dl─ů jp─Öwis^jo t┼Ťft! przeds
P1110219 W przypadku gdy metoda proporcjonalna b─Ödzie stosowana na koniec okresu sprawozdawczeg
Technika i pomiary bada┼ä stanowiska. Generator ma┼éych k─ůt├│w przedstawiony jest na zdj─Öciu na str.
32083 pict0003 (9) Teorii prawdopodobie┼ästwu opirti na poj─Öciu cz─Östo┼Ťci wzgl─Ödnej Teoria ta oparta
wi─Öcej podobnych podstron