IMG�65 (2)

słony, czyli będzie niepewny W następstwie tego obliczona składowa reaktancyjna będzie tak samo mało dokładna To zadanie można by rozwiązać najskuteczniej, gdyby wydzielić fizycznie (mówi się analogowo) składową reaktancyjną napięcia¹ i tę składową np zmierzyć bezpośrednio I tak się robi, do czego wrócimy.

Idea zawarta w schemacie przedstawionym na rys. 4 4b, zastosowana do przetwarzania rezystancji na napięcie przy prądzie stałym, jest również wykorzystywana przy prądzie przemiennym w technice cyfrowej do pomiaru w ogólnym przypadku składowych impedancji W tym celu zamienia się w układzie napięcie probiercze stałe (napięcie pomiarowe impedancji) na napięcie zmienne (UJ) o danej częstotliwości, dodaje się układ wydzielania składowych napięcia (czynną i bierną) i układ prostowania napięcia zmiennego, bo w zastosowanym przetworniku a/c mierzy się napięcie stałe Na rysunku 4 9a przedstawiony został schemat ideowy układu, w którym realizuje się wymienione funkcje i za pomocą którego można mierzyć każdą ze składowych impedancji (przy prądzie przemiennym)

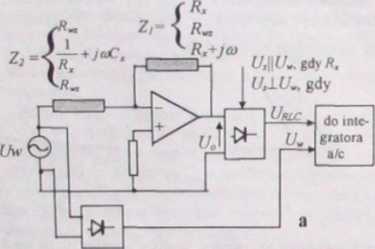
Rys. 4.9. Przetwornik składowych impedancji: a - schemat ideowy; b - wykres wektorowy

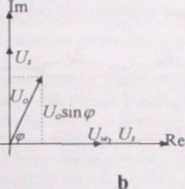
Układ pokazany na rys 4 9a działa następująco Jako impedancję Z/ w pętli sprzężenia zwrotnego wzmacniacza łączy się albo R,, albo /?„, albo R, + jcuL zależnie od realizowaną funkcji pomiarowej Wówczas jako Z» na wejściu wzmacniacza muszą być połączone odpowiednio albo /?„, albo y„+jaiC_x, albo R_m Składową czynną impedancji kondensatora wygodnie jest widzieć jako konduktancję a nie jako rezystancję. Napięciem wymuszającym prąd w impedancji (napięciem probierczym) jest napięcie sinusoidalne t/„ o częstotliwości 1000 Hz. bo taka częstotliwość jest znormalizowaną częstotliwością odniesienia przy pomiarach impedancji (oczywiście - częstotliwość może być też inna). To samo napięcie (/„ jest również prostowane, filtrowane i jako wartość średnia doprowadzone do integratora przetwornika analogowo-cyfrowego o podwójnym całkowaniu (gdy taki jest zastosowany), albo jest mierzone, gdy potrzebny odpowiedni iloraz wartości napięć wyznaczany jest numerycznie. Na wyjściu wzmacniacza jest zastosowany prostownik fazoczuły². Napięcie sterujące U, prostownika fazo-czułego jest albo przesunięte o "/? w stosunku do napięcia probierczego (/„ dla funkcji pomiarową C_M lub L„ albo może być w fazie z tym napięciem dla funkcji pomiarowej R, (gdyby miała być mierzona tylko „czysta rezystancja" prostownik nie musiałby być fazoczuły) Na

Byłaby to realizacja metody różnicowej (którą już wielokrotnie przywoływaliśmy), tyle że trzeba by tu realizować różnicę wektorową

Prostownik fazoczuły inaczej - prostownik sterowany Układowo jest tożsamy z detektorem (azoczułym (patrz rys 3.5).

wyjęciu prostownika fazoczułego otrzymuje się napięcie, które jest składową bierną Umr napięcia U_m, gdy U,±U_W (rys 4 9b) lub składową czynną, gdy jest przeciwnie Równaniem przetwarzania prostownika fazoczułego jest bowiem zależność L/»cos((/,,(/»), gdzie pod znakiem cosmusa występuje kąt między U, i U_c Z napięcia wyprostowanego jest odfiltrowana składowa zmienna Wyznaczanie stosunku odpowiedniej składowej do napięcia (/„ realizuje się w przetworniku a/c o podwójnym całkowaniu (można by też mierzyć i rachunki wykonać numerycznie).

Rozpatrzymy kolejno funkcje pomiarowe realizowane w układzie Gdy mierzona jest rezystancja R., to na wejściu wzmacniacza włączone jest R_m i układ działa tak jak na rys 4 4b wg równania (4 7), tylko rezystancja mierzona jest przy napięciu probierczym przemiennym

Gdy mierzona jest pojemność C„ to odpowiednio stosując zależność (4 7) otrzymamy (uwzględniamy bowiem zespolony sens zmiennych):

*,;(J-+y«ę,). gŁĘpydif)

Po przekształceniu i porównaniu części urojonych otrzymamy zależność:

■ t/.tinp, I Uuc    .....

* U_w o>H„    <u/<„ U,    U. ¹

w której występuje współczynnik stały i stosunek zmiennych wyznaczany w przetworniku a/c o podwójnym całkowaniu lub numerycznie W stałej miernika musi być uwzględnione skalo* wanie ze względu na wartość tu i R„

Porównując składowe rzeczywiste lewej i prawej strony możemy otrzymać

I _c l U cos <p _ 1 Uklc

R. * Rm V. " u.

albo

U_m m u_m

t/.eosr ⁼ “ V_MX:

(4 16)

zależnie od tego, za pomocą jakiej wielkości chcemy wyrazić niedoskonałość kondensatora (np czy przewodność, czy rezystancję jego izolacji)

Podobnie jak dla pojemności C, można wyprowadzić zależność dla indukcyjności

_ R„ U, siny ₌ R_m V^ * to U_w w U_w

oraz

R. =R„

U„ cotp

W.

V_w

(4 17)

We wszystkich podanych zależnościach trzeba zrealizować dzielenie dwu napięć stałych, żeby otrzymać wynik przetwarzania danej składowej impedancji Dzielenie to - jak wiemy - realizuje się w sposób naturalny i prosty analogowo w przetworniku a/c o podwójnym całkowaniu. Dzielenie takie można wykonać numerycznie, co może być racjonalne, gdy miernik jest z innych powodów zmikroprocesorowany. W każdym przypadku - analogowo lub numerycznie - z zależności (4 15) i (4.16) (4 17) można zbudować dokładniejszy miernik składowych impedancji niż na zasadzie numerycznej z zależności (4 12) i (4 13), ponieważ wydzielenie odpowiednich składowych napięcia w układzie z rys.4 9 osiąga się za pomocą działań „analogowych" bezpośrednio na odpowiednich napięciach a me w wyniku działań numerycznych na liczbach przybliżonych. Oczywiście, zakładamy jednakową staranność realizacji funkcji cząstkowych

Przedstawione sposoby cyfrowego pomiaru składowych impedancji stosowane są raczej do pomiaru danej, jednej składowej impedancji, tej dominującej, a me obu składowych tej samej impedancji. Oferowane rozwiązania nie są zbyt dokładne, ale są łatwe w realizacji i

207