MF dodatekA28

Aneks A .7

Średnie ważone

273

Można wykazać, że otrzymany w ten sposób ciąg punktów {x_n} jest zbieżny do pierwiastka Xq równania f(x)=0. Dla oszacowania błędu bezwzględnego przybliżenia

x = x_n można skorzystać ze wzoru

|x-x₀

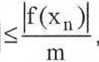
A(7.7)

gdzie: |f'(x)>m>0 dlaxe<a,b>|

Jeżeli założymy, że pochodna f’(x) nie zmienia znaku i jest ciągła w przedziale

<a, b>, to błąd bezwzględny przybliżenia x = x_n możemy również wyznaczyć ze wzoru

x-x_n <

M-m

m

x„~x

n-1 »

A(7.8)

gdzie: 0<m<|f'(x)|<M dla xe<a,b>.

W podręcznikach metod numerycznych przedstawione są również inne szybciej zbieżne, ale o wiele bardziej skomplikowane, metody przybliżone obliczania pierwiastków danego równania f(x)=0.

8. Średnie ważone

Niech będą dane dwa ciągi skończone liczb dodatnich

a={a₁,a₂,...,a_n} i w = {w,,w₂,... w_n}. Wówczas wyrażenia

A(8.1)

A(8.2)

A(a;w)= ^wl^al^+w2^a2⁺ ■^+wn^an ₁ W|+W₂+ ... + w_n

G(a;w) = (a,^Wl ... a*" )^wi+-w_n ,