Odpowiedzi2 (2)

Zadania powtórzeniowe, s. 22-25

14. b)

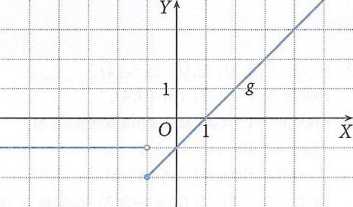
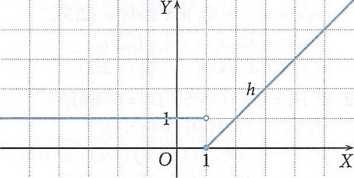
15. a) D = (-4; oo), g(D) = (1;7>

b) D = <-6;oo),^(D) = (-3;3)

c)    D = (-4; oo), g(D) = {-3;3)

d)    D=(-oo;4),*(D) = (-3;3>

Zestaw B - odpowiedzi

1. A 2. B 3. A 4. D 5. D

Zestaw C-odpowiedzi

1.    D = R \ {-5}, /(O) =/(5) =0

2.    D = (4; 6}

3.    /(x)=x²-l,/_min(0) = -l

4.    a) /(-\/2) = -2\fl b)/(2V^/3) = 24\/3

5.    Dg = (—oo; l), g(Dg) = (—5; l)

6.    /(x) = |x| + 3

7.    /(D) = {l,2,3,4}

8.    ^(x) = 2x-6

Zestaw D- odpowiedzi

1.    a) /(15) =3, /(93) = 1,/(102) = 2

2.    c) -1, 0, 1, 2, 3, 4

3.    a) D = <-5;0)u<l;6> b) f(D) = {-2;3> c)x = -lłubx = 2 d) x e {-5;0} u (1;5)

4.    g(D) = (-8;0>, ^(V2-l) = 2x/2-4

5.    D = <-3;5),_<g(D) = <-l;2), *(-l)=*(2)=*(5) = 0

6.    (-6,4) i (2,4)

Zestaw C - modele rozwiązań zadań otwartych

Numer zadania	Etapy rozwiązania zadania
Wyznaczenie dziedziny funkcji: D = R \ {-5}
1 .	Wyznaczenie miejsc zerowych: x = 0, x = 5
2.	Zapisanie układu nierówności: f x-4^0 |6-x^0
	Rozwiązanie układu nierówności i podanie odpowiedzi: D - (4; 6)
3.	Podanie wzoru funkcji f: /(x) = x^2 - 1
	Wyznaczenie najmniejszej wartości funkcji /: /mjn = -1
4. a) 4. b)	Obliczenie / (—s/2): / (-\/2) = -2y/l
	Obliczenie / (2\/3): / (2\/3) = 24\/3
5.	Wyznaczenie dziedziny funkcji g: Dg = (-oo; 1)
	Wyznaczenie zbioru wartości funkcji g: g(Dg) = (-5; 1)

164