81642 Odpowiedzi1

Zadania powtórzeniowe, s. 32-34

Numer

zadania

Etapy rozwiązania zadania

Naszkicowanie w jednym układzie współrzędnych prostych: k, l, m, n

4. c)

|—

6.

L

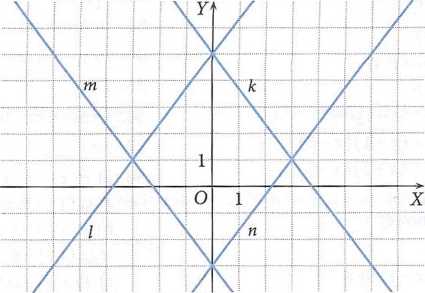
Zauważenie, że figura jest rombem i obliczenie jej pola: P - 24

Wprowadzenie oznaczeń: s - droga między domem a szkołą, x - droga przebyta przez dziewczynki do momentu spotkania, V\ - średnia prędkość Ali w km/min, v₂ - średnia prędkość Oli w km/min, t - czas jazdy Ali do momentu spotkania, s > 0, t > 10 i zapisanie wzorów: V\ = v₂ = ^

Zapisanie wzoru na drogę przebytą przez dziewczynki: v\t = x, v₂(t- 10) = x

Ułożenie równania: ^=^j(f~10)

Rozwiązanie równania: t- 20 i podanie odpowiedzi: Ola wyprzedzi Alę o godzinie 7.20. Zapisanie równania: m + n= 140 Zapisanie równania: m + 15n = 980 Rozwiązanie układu równań: m - 80, n = 60

5. Funkcja kwadratowa

Zestaw A-odpowiedzi

1.    a) y = ~\x² + 1 b) y = -j(x-l)² c) y = -|(x + 3)²-2

2.    a) f(x) = -(x-2)², f(D)= (~oo;0>

^b)    /(*) = {x + 3)² - 9, f(D) = (-9; oo)

c)    f(x) = 2(x - l)² + 2, f(D) = (2; oo)

3.    a) (1,0), (3,0), (0,3),

f(x) = (x-l)(x-3) = (x-2)²-l

b)    (1,0), (-5,0), (0,5),

f(x) = -(x- l)(x + 5) = ~(x + 2)² + 9

c)    (0, —3), f(x) = -2(x - l)² - 1, nie ma postaci iloczynowej

4.    a) / maleje w (-oo; 12), rośnie w (12; oo),

/(£>) = <- 29; ~)

b)    / rośnie w (-oo;-|), maleje w (-|;oo),

/(D) = (-oo;12i>

c)    / maleje w (-oo;2\/2), rośnie w (2y/2; o°), /(D) = <-10;oo)

5.    a) fi = 0, C = 2, Alin ⁼ 2 b) fi = 0, C = 0, Anin — 0

c) fi = —8, C = 13, Anin ⁼ 5 d) fi — 4, C = —1, Anin ⁼ ~3

6.    a) c = -3, /(*) = ~(x — 1 )² — 2

b)    c = -1, f(x) = ~(x-l)²

c)    c = 3, /(*) = ~{x - l)² + 4

d)    c = 3^2-1, /(x)--(x-1)² + 3\/2

171