82495

Część 2 16. ZADANIA POWTÓRKA 35

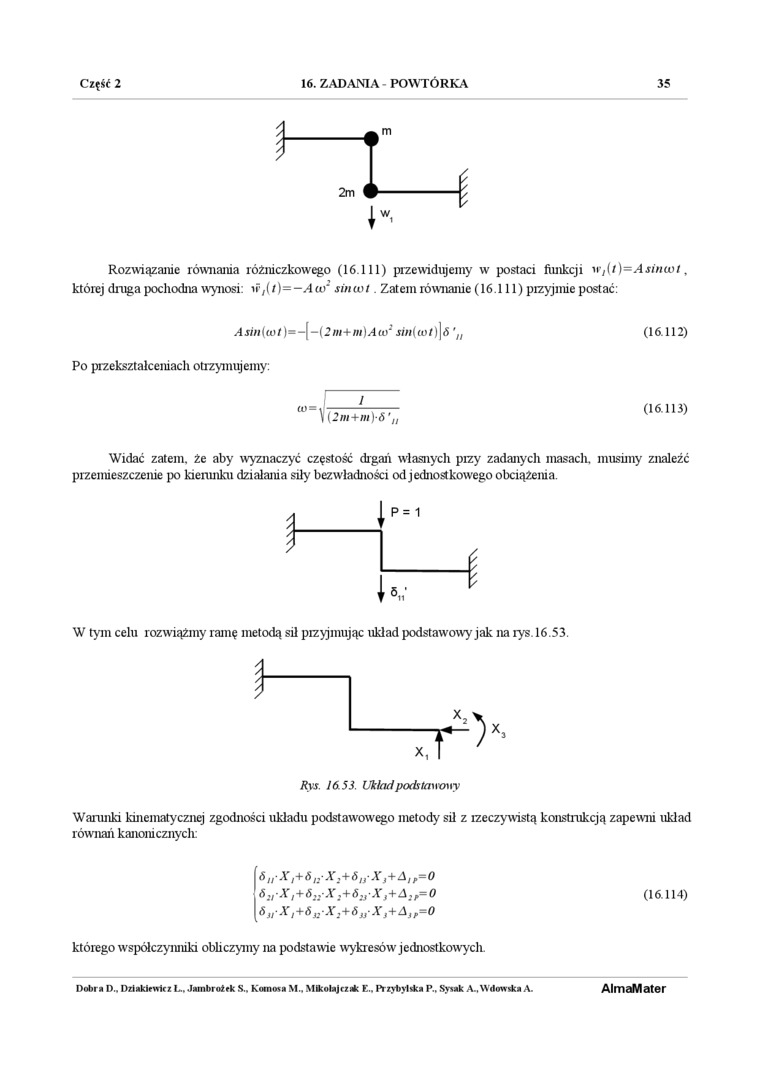
i

2m

Rozwiązanie równania różniczkowego (16.111) przewidujemy w postaci funkcji n,{t)=Asiniot, której druga pochodna wynosi: i?,(/ )= -A to^: sin co i. Zatem równanie (16.111) przyjmie postać:

(16.112)

Asin(tot)=-\-(2m+m)Ato^: j//i(a>/)]ó *_n Po przekształceniach otrzymujemy.

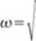
(2m+ni)S'_n

(16.113)

Widać zatem, że aby wyznaczyć częstość drgań własnych przy zadanych masach, musimy znaleźć przemieszczenie po kierunku działania siły bezwładności od jednostkowego obciążenia.

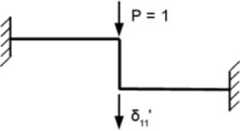
W tym celu rozwiążmy ramę metodą sil przyjmując układ podstawowy jak na rys. 16.53.

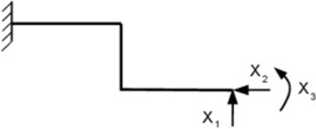
Rys. 16.53. Układ podstawowy

Warunki kinematycznej zgodności układu podstawowego metody sił z rzeczywistą konstrukcją zapewni układ r ównań kanonicznych:

6 //• X/+6 X ,+6_1}-X _s+A, p⁼0

S,,X ,+6_::X    f+A, f — 0    (16.114)

6j,X _t+6 _J2'X 2+ó_JyX _J+A_sf⁼0

którego współczyrmiki obliczymy na podstawie wykresów jednostkowych.

AlmaMater

Dobra D.. Dztakicwlcz L.. Jatnbroźrk S.. Ko«n<na M„ Mikołajczak E„ Przybylłka P.. Syrak A , Wilmwka A.