Untitled 35

3. Przybliżone rozwiązywanie równań nieliniowych i ich układów 140

3.2.4. Lokalizacja zer zespolonych

Podamy teraz kilka twierdzeń pozwalających oszacować moduł zespolonych zer wielomianu.

Tw. 1. (Cauchy’ego). Niech

f(z) = a₀zⁿ + aizⁿ-'+ ... + a_n, a₀ # 0

oraz

n

F(z) = \a₀\zⁿ - £ |a_k\zⁿ~^k    (3.37)

k= 1

Jeżeli a oznacza jedyne dodatnie zero rzeczywiste wielomianu F(z), zaś z_u z₂, ..., z_n są zerami wielomianu f(z), to

\z_k\ < a dla k = 1, 2, ..., n

Uwaga. Współczynniki a_k mogą być zespolone.

n

Tw. 2. Niech f(z) = £ a_kzⁿ~^k, a₀ = 1, i niech fi będzie dowolną liczbą k = o

dodatnią. Wszystkie zera wielomianu spełniają nierówność

|z*|<y    k=\, 2, ...,n    (3.38)

gdzie

y = max ^1/jS, £ \a_k\p^k~'^

Przykład 1. Znaleźć oszacowanie modułów zer wielomianu /(z) = z⁴ + 3z* — 5z + 1

Szukane oszacowanie y = max (1//?, 3/? + 5 fi² + fi²). Trzeba tak dobrać fi, aby y było możliwie małe. Przyjmijmy fi = 1/2. Mamy ,1 ¹¹

3--+5-- + -= 2,875 oraz 1 /fi = 2. Moduły zer badanego wielomianu /(z) są mniejsze niż 2,9.

n

Tw. 3. Niech /(z) = £ a_kz"~^k, a₀ / 0. Wszystkie zera wielomianu f(z)

k = 0

spełniają nierówność

\z_k\ ^ 1 -f max

K n

Ok

a₀ ’

k = 1,2, ..., n

(3.39)

Uwaga. Współczynniki a_k mogą być zespolone.

Następne dwa twierdzenia dotyczą wielomianów o dodatnich rzeczywistych współczynnikach.

n

Tw. 4. Moduły wszystkich zer wielomianu f(z) = £ a_kz^{n k} spełniają

nierówność

(

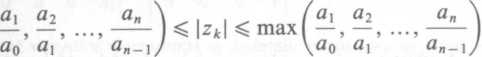
n

min (

(3.40;

Tw. 5. Jeżeli współczynniki wielomianu f(z) = JT a_kz” ^k spełniają wa runek a₀> a_x> a₂> ... > a_n> O, to moduły wszystkich zer wielomianu f(z są mniejsze niż 1. Jeżeli a„> a„_i > ... > a_x > a₀ > O, to moduły wszystkicl zer wielomianu f(z) są większe niż 1.

Często ważnym zagadnieniem jest dla nas lokalizacja zer wielomianu n; płaszczyźnie zespolonej. Na przykład, badanie stabilności liniowych układóv automatyki, równań różniczkowych zwyczajnych czy różniczkowo-całko wych wymaga rozstrzygnięcia, czy wszystkie zera danego wielomianu maj ujemną część rzeczywistą. Podamy teraz trzy kryteria: Michajłowa (grafic2 ne), Routha i Hurwitza, określające warunki, przy których wielomia o współczynnikach rzeczywistych ma zera położone na lewo od osi urojone

Kryterium Michajłowa. Warunkiem koniecznym i dostatecznym na to, ab zera wielomianu/(z) miały ujemną część rzeczywistą, jest, by wektor o początk w punkcie (0, 0) i końcu w punkcie f(jt) zatoczył kąt nn/2, gdy t zmienia się c 0 do +oo, przy czym krzywa zataczana przez koniec wektora nie moi przechodzić przez początek układu.

W celu sformułowania kryterium Routha rozważmy wielomian

(3.4

f(ź) = a₀zⁿ + b₀z^{n 1} + atz" ² + b_lz" ³ + ... o współczynnikach rzeczywistych. Obliczamy wartości

<

k = 0, 1, ..., r — 1, b₀ć 0

k = 0, 1, ..., r — 1,    co # 0

= Ck+i ~ -j d_k+i, k = 0, 1, ..., r-2, d₀ć 0

“o

i ustawiamy je w postaci tablicy

^a0i 0\, 0-2, ..., a_T b₀, b_u b₂, ..., b_r ^c0> Cj, c₂, ..., C_r_i

d₀, d\, d₂, ..., ć/_r_i ^eo> Ci, e₂, e_r_₂

(3-“