Untitled 30

130

J. Przybliżone rozwiązywanie równań nieliniowych i ich układów

Przy rozwiązywaniu równań metodą stycznych wygodnie jest skorzystać z następującego twierdzenia, które podamy tutaj bez dowodu.

Tw. Jeżeli mamy przedział <a; bj taki, że:

(i)    /(a) i f{b) mają przeciwne znaki,

(ii)    /"(x) jest ciągła i nie zmienia znaku na <a; bj,

(iii)    styczne do krzywej y =/(x) poprowadzone w punktach o odciętych

aib przecinają oś OX wewnątrz przedziału    bj, wówczas równanie f(x) = 0

ma dokładnie jeden pierwiastek a w przedziale bj i metoda Newtona jest zbieżna do a dla dowolnego punktu startowego x₀e(a; bj.

Znanym przykładem zastosowania metody Newtona jest algorytm obliczania pierwiastka kwadratowego. Pierwiastek kwadratowy z liczby dodatniej c jest dodatnim pierwiastkiem równania

x² — c = 0

Mamy tutaj /(x) = x² — c i f'(x) = 2x, zatem na podstawie wzoru (3.18)

X²n — C

x_n+] = x„--ⁿ--(x_n ^ 0) i po uproszczeniu otrzymujemy

zx_n

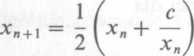
Wszystkie założenia powyższego twierdzenia są spełnione na przedziale {a; bj takim, że 0 < a < c^1/2 i b > ^(a + c/a).

Dotychczasowe rozważania prowadziliśmy przy założeniu, że szukany pierwiastek a jest pojedynczy. Omówimy teraz pokrótce przydatność poszczególnych metod w przypadku, gdy a jest pierwiastkiem wielokrotnym. Przypomnimy najpierw definicję wielokrotności pierwiastka.

Def. Liczbę a nazywamy r-krotnym (r > 2) pierwiastkiem równania f{x) = 0 wtedy i tylko wtedy, gdy jest (r — l)-krotnym pierwiastkiem równania f\x) = 0.

Jeżeli a jest pierwiastkiem o parzystej krotności, to metoda połowienia, omówiona w p. 3.1.1 traci sens, natomiast dla krotności nieparzystej (r ^ 3), gdy /(a) f(b) < 0 pozostaje słuszna. Podobnie przedstawia się sprawa dla metody reguła falsi oraz metody siecznych, przy czym dla tej ostatniej obniża się rząd metody (uwagi dotyczące rzędu metody są opisane w p. 3.1.5). Metoda Newtona pozwala na znalezienie pierwiastka zarówno o nieparzystej, jak i o parzystej krotności, jeżeli tylko istnieje odpowiednie lewo- lub prawostronne sąsiedztwo szukanego pierwiastka o stałym znaku pierwszej i drugiej pochodnej, lecz tu także obniża się rząd metody.

Stosuje się również pewne modyfikacje omówionych metod pozwalające utrzymać ich rząd, a więc przyspieszające ich zbieżność. Jednym ze sposobów takiej modyfikacji jest przekształcanie zależności (3.18) do postaci

(3.21)

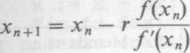
gdzie r jest krotnością pierwiastka (znaną a priori). Ponieważ na ogół krotność pierwiastka nie jest znana, często we wzorach (3.13) i (3.18) stosuje się podstawienie: zamiast funkcji f(x) wprowadza się funkcję

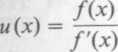
(3.22)

Równanie u(x) = 0 ma identyczne pierwiastki jak równanie (3.1), ale wszystkie te pierwiastki są pojedyncze. Wzory (3.13) i (3.18) przyjmują wtedy postać

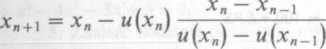
oraz

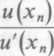
(3.13a)

(3.18a)

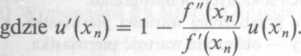
Przykład 2. Znaleźć pierwiastek równania x⁴ — 4x³ — 5x² — 4x + 4 = 0

za pomocą: a) metody Newtona (wzór (3.18)), b) zmodyfikowanej metody Newtona dla r = 2 (wzór (3.21)) i c) zmodyfikowanej metody Newtona wykorzystującej podstawienie (3.22).

Mamy

/(x) = x⁴ - 4x³ + 5x² - 4x + 4 = (x - 2)²(x² + 1) f\x) = 4x³ - 12X² + 10x - 4 /"(x) = 12x² - 24x + 10

«

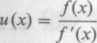
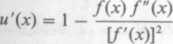
i jako x₀ przyjmujemy 3.

W tablicy 3/5 są zestawione wyniki otrzymane wszystkimi trzema metodami. Jak należało oczekiwać, zbieżność metod b) i c) jest znacznie szybsza niż metody a).

Przykład 3. Napisać program obliczania przybliżonej wartości pierwiastka równania /(x) = 0 z zastosowaniem metody Newtona (wzoru (3.18)).

/(•*.)

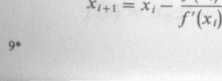
dla i = 0, 1, 2, ...