Untitled 31

132

3. Przybliżone rozwiązywanie równań nieliniowych i ich ukiadów

3/5

X,	Metoda a)	Metoda b)	Metoda c)
*1	2.6156	2.2308	1.7963
*2	2.3601	2.0183	1.9814
*3	2.2007	2.00921	1.9997
*4	2.1081	2.00462
*5	2.0562	2.00232
*6	2.0287
*7	2.0146
*8	2.00733
*9	2.00368

Procedura iteracyjna jest przerywana, gdy po obliczeniu jc_/+l |delta| < = EPS oraz    [/(*,+,)| < = 100 * EPS

gdzie EPS jest zadaną dokładnością a

dla

dla

l*,+il > 1 l*/+il <= 1

f *<+i ~x,

delta = j *i+i

X,_{+ l}-X,

Opis parametrów formalnych oraz zmiennych lokalnych podprogramu:

*    — punkt startowy obliczania przybliżonej wartości pierwiastka, a po zakoń

czeniu działania procedury — obliczona wartość pierwiastka,

EPS    — dokładność obliczeń,

n    — maksymalna liczba iteracji,

err    — parametr wyjściowy, sygnalizacja    błądów:

0    — brak błędów,

1    — nie osiągnięto wymaganej dokładności w n krokach iteracji,

2    — w trakcie obliczeń wartość pochodnej funkcji / była bliska lub równa

zeru,

F(x, fx, fxx) — procedura zdefiniowana w bloku zewnętrznym programu obliczająca wartość funkcji fx i wartość pochodnej tej funkcji fxx w punkcie x.

Tekst programu:

PROCEDURĘ NEWTON(VAR x:real; epstreal; minteger; VAR err:byte); VAR t,fx,fxx,dx,delta: real;

i: integer;

BEGIN

err:=0;

F(x,fx,fxx);

{ początek procedury iteracyjnej }

FOR i : = 1 TO n DO BEGIN

IF fx = 0 THEN EXIT;

IF (ABS(fxx) - l.E-6) < = 0 THEN BEGIN err := 2;

EXIT;

END;

dx := fx/fxx; t :- x;

3.1. Jedno równanie z jedną niewiadomą

133

x := x - dx;

F(x,fx,fxx);

{ badanie dokładności } delta := ABS(x - t);

IF ABS(x) > 1 THEN delta := delta/ABS(x);

IF ABS(delta) <= eps THEN IF ABS(fx) <= 100»eps THEN EXIT;

END;

err := 1;

END;

Ćwiczenia

1.    Omówić metodę Newtona i podać błąd n-tego przybliżenia.

2.    Udowodnić wzór (3.18).

3.    Znaleźć pierwiastki równań z ćwiczenia 7 w p. 3.1.1 metodą Newtona.

4.    Stosując metodę Newtona znaleźć pierwiastki równań: a) r³ — 2x + 1 = 0, b) x* + + X³ — 4JC² — 3x + 3 = 0,

5.    Znaleźć dodatnie pierwiastki równania e* — 3x¹ = 0 metodą Newtona.

6.    Korzystając z metody Newtona znaleźć wzór rekurencyjny na obliczanie pierwiastka sześciennego z liczby dodatniej c. Wykonać kilka kroków obliczenia dla c = 10.

7.    Stosując metodę Newtona do równania x" — c = 0, wyprowadzić wzór na obliczanie pierwiastka n-tego stopnia z liczby dodatniej c.

8.    Odwrotność liczby N można obliczyć za pomocą algorytmu iteracyjnego Xi+i = x,(2 - Nx,)

a) Wyprowadzić ten algorytm stosując metodę Newtona do funkcji

/(*) =--N x

b) Zaczynając z punktu x₀ = 0,2 obliczyć tym algorytmem odwrotność liczby N = 4.

9. Co się stanie, jeżeli we wzorze (3.20) wybierzemy x₀ < 0?

10.    Równanie X² — 4x + 4 = 0 ma pierwiastek podwójny x₀ = 2. Zaczynając z punktu jcj = 1 obliczyć przybliżoną wartość pierwiastka: a) metodą Newtona, b) zmodyfikowaną metodą Newtona według (3.21) i c) zmodyfikowaną metodą Newtona z podstawieniem (3.22).

11.    Wyjaśnić, dlaczego metody reguła falsi i metody siecznych nie można stosować do obliczania pierwiastków o parzystej krotności.

12.    Narysować schemat blokowy programu obliczania przybliżonej wartości pierwiastka (pierwiastków) równania f(x) = 0 metodą Newtona.

Odpowiedzi. 4. a) -1,618034; b) -1,732, -1,618, 0,618, +1,732. 5. 0,91001; 3,73308.

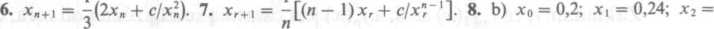
= 0,2496; x, = 0,24999936, ... 9. Otrzymamy procedurę zbieżną do — *J~c.

3.2. METODY POSZUKIWANIA ZER WIELOMIANÓW

Opisanymi w poprzednich punktach metodami można rozwiązywać dowolne równania zarówno algebraiczne, jak i przestępne, a po pewnych prostych modyfikacjach można również znajdować pierwiastki zespolone (z wyjątkiem metody reguła falsi). W przypadku równań algebraicznych

/(z) = a₀zⁿ + a_xz" ¹ + ... + a„_iZ + a_n = 0 (3.23)