Untitled 34

138

3. Przybliżone rozwiązywanie równań nieliniowych i ich układów

Tw. (Lagrange’a). Niech a₀ # O / a_k(k ^ 1) będzie pierwszym ujemnym współczynnikiem wielomianu (3.26). Wszystkie dodatnie zera tego wielomianu są mniejsze niż

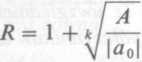
(3.29)

gdzie A oznacza maksimum modułu ujemnych współczynników wielomianu.

Jeżeli wszystkie współczynniki wielomianu są nieujemne, to nie ma on zer dodatnich.

Należy pamiętać, że wyznaczenie przedziałów, w których mogą znajdować się zera rzeczywiste, nie oznacza bynajmniej, że wielomian ma takie zera. Ma je na pewno każdy wielomian nieparzystego stopnia.

Przykład 1. Wyznaczyć przedział zawierający wszystkie zera rzeczywiste wielomianu f(x) = 2x^> + *⁷-*⁵ + 6x³- l2x² + 9

Pierwszy ujemny współczynnik występuje przy X⁵, czyli jest to a₄. Stąd mamy, że k = 4. Największy co do modułu ujemny współczynnik wynosi —12, czyli A = 12. Mamy więc

R = 1 + 4= 1 +    « 2,565

Zgodnie ze wzorami (3.28) obliczamy

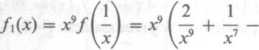
^{1 6} 12

? ⁺ ?“7 ^{+ 9l =}

= 9x⁹ - 12*⁷ + 6x⁶ - x* + X² + 2 f₂(x) = f(-x) = -2x⁹ - X¹ + x⁵ - 6x³ -12^ + 9

= 9x* - 12*⁷ -6x⁶ + x*-x² + 2x⁹

We wszystkich trzech przypadkach pierwszy ujemny współczynnik występuje przy x⁷, czyli jest to a₂- Stąd mamy k = 2. Największy co do modułu ujemny współczynnik jest również we wszystkich trzech przypadkach równy —12, czyli A = 12. Zatem

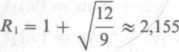
*2= 1 +

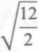
« 3,449

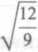
w 2,155

Ry= 1 +

Tak więc dodatnie zera należą do przedziału (0,464; 2,565), a ujemne do przedziału ( — 3,449; -0,464).

3.2. Metody poszukiwania zer wielomianów

139

3 2.3. Metody przybliżonego obliczania zer rzeczywistych wielomianu

Istnieje wiele metod znajdowania pierwiastków rzeczywistych równania (3.23) (patrz np. [17, 50, 62]). Przytoczymy tutaj w skróconej formie metodę iterowanego dzielenia.

Dzieląc wielomian f{x) przez czynnik liniowy (x — Xj) otrzymamy

/(x) = (x — Xj)(b₀xⁿ~' + bixⁿ~² + ... + b„_,) -I- Rj    (3.30)

gdzie reszta Rj jest równa f(xj). Współczynnik b_k obliczamy ze wzoru rekurencyjnego

b₀ = a₀, b_k = a_k +Xjb_k_i dla k=l,2,...,n    (3.31)

i stąd

Rj = b_n = a_n + x_jb„__]    (3.32)

Powtórne podzielenie przez (x — Xj) da nam

f(x) = (x — Xj)²(c₀xⁿ~² + C\Xⁿ~³ + ... + c„_₂) + (* — Xj)Rj + Rj (3.33) przy czym R) = /'(*,) oraz ^co — bo — a₀

c_k = b_k + x_tc_k-u k = 1, 2, ..., n - 1    (3.34)

Rj= c_n _ i = 6„_, +XjC_n. ₂

Do obliczania kolejnych wyrazów ciągu przybliżeń (x_k), k= 1, 2, ..., j, rzeczywistego pierwiastka równania (3.23) możemy zastosować: metodę siecznych

X_j+l=Xj-

Rj(^xj — ^xj+\)

^Ri ~ ^Rj-\

(3.35)

«

(należy tutaj przyjąć początkowe przybliżenia X] i jc₂) lub metodę Newtona

^Xj+l — Xj —

Ri

^Rj

(3.36)

(należy tutaj przyjąć przybliżenie początkowe Xi). Oczywiście każdy ze wzorów (3.35) i (3.36) można stosować wielokrotnie, tworząc ciąg kolejnych przybliżeń dzielnika aż do uzyskania dwóch kolejnych wartości x_k i x_{k + ]} możliwie bliskich.

Ćwiczenia

1. Korzystając ze wzorów (3.35) i (3.40) znaleźć rzeczywiste zero wielomianu f(x) = = X³ — x — 1, przyjmując jako przybliżenie początkowe odpowiednio: x, = 1,2 oraz x₂ = 1,3 w metodzie siecznych, a x, = 1,3 w metodzie Newtona.