Untitled 38

3. Przybliżone rozwiązywanie równań nieliniowych i ich ukiadów 146

gdzie

r = —Pk^cn-1 + <łk^cn- 3

s = d-2 - rc„-i

Algorytm Q-D. Omówione powyżej metody wymagają określenia wartości początkowych dostatecznie bliskich wartości szukanego pierwiastka lub współczynników czynnika kwadratowego. Algorytm Q-D umożliwia znalezienie pierwiastków wielomianu bez potrzeby określania wartości początkowych.

Dla wielomianu (3.23) tworzymy tablicę czynników q i e, której pierwsze dwa wiersze (patrz tabl. 3/8) oblicza się ze wzorów

?^(1) = ~a2/au	pozostałe q^(i) =	0	dla 1 = 2,.	.., n
e^(i) = ai + 2/ai+u	i = 1, 2, ..., n	- 1
O II II						(3.53)
3/8
e(0) qn)	e(U q(2)	em	<j^(3)		qw	e<">
—a, 0	0 <H ^ai		0	^an ^an-l	0	0

W następnych wierszach tablicy wartości q oraz e oblicza się ze wzorów

q(>) — _e(i) _ gO-1) _|_ q(o

g(0 ₌ (₉(« + i)/₉<0)_e.    (3.54)

w których wartości e i q po prawych stronach równości (3.54) są brane z poprzedzających wierszy tablicy. Obliczenia kontynuuje się tak długo, aż wartości e staną się bardzo bliskie zeru. Wówczas wartości kolejnych q‘ są wartościami pierwiastków.

Jeżeli wielomian ma parę zespolonych, sprzężonych pierwiastków, to jedna z wartości e nie będzie dążyła do zera. W takim przypadku suma wartości q leżących po obu stronach tego e daje wartości — r, a iloczyn dwóch czynników q, lewego leżącego powyżej oraz prawego leżącego poniżej, daje wartości s czynnika kwadratowego x² + rx -I- s. W przypadku pierwiastka podwójnego postępuje się identycznie. Gdy chociaż jeden ze współczynników a, jest równy zeru, wówczas nie można obliczyć q i e z pierwszych wierszy. W takim przypadku należy wprowadzić nową zmienną, np. y — x — 1 (dobór współczynnika jest dowolny).

Przykład. Stosując metodę Q-D znaleźć pierwiastki równania x⁴ - 6xⁱ + I2x² - 19* + 12 = 0

3.2. Metody poszukiwania zer wielomianów

147

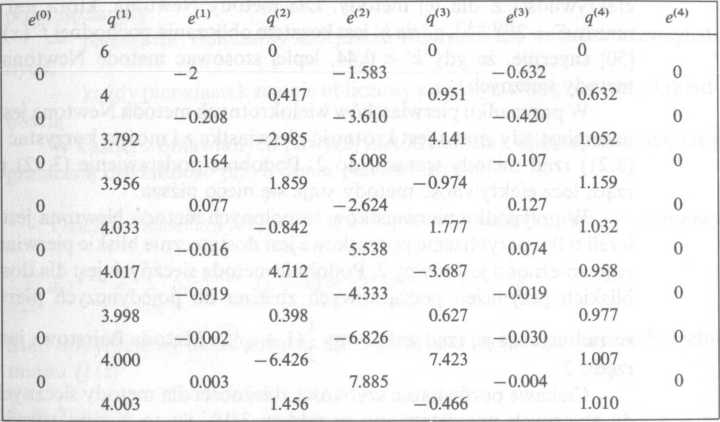
W tablicy 3/9 zestawiono wyniki kolejnych obliczeń. Jak widać q^m jest zbieżne do 4, q^w do 1. Ponieważ e^m nie jest zbieżne do zera, więc q^m i q^m reprezentują czynnik kwadratowy

_{r =} _(_?<2) + ₉0>) = -(1,456 - 0,466) = -0,990 j = (-6,426) (-0,466) = 2,995

Czynnik kwadratowy ma postać x² - 0,99x + 2,995

Zgodność, jak widać, jest zupełnie dobra, gdyż badany wielomian można rozłożyć na czynniki x* — 6x³ + 12x² — 19x + 12 = (x — l)(x - 4)(x² — x + 3)

3/9

3.3. UWAGI O EFEKTYWNOŚCI METOD PRZYBLIŻONEGO OBLICZANIA < PIERWIASTKÓW

Dla użytkownika istotny jest problem jakości poszczególnych metod. Każdej metodzie można przyporządkować liczbę p (największą możliwą dla danej metody) — zwaną wykładnikiem zbieżności danej metody. Mówimy, że metoda jest rzędu p, jeżeli istnieje stała K taka, że dla dwu kolejnych przybliżeń x_k i x_k + j zachodzi nierówność

|x* _{+ 1} - x| ^ K\x_k - x\^p

Można porównywać rzędy metod określające szybkość ich zbieżności, można także porównywać ich efektywność, która określa zakres obliczeń koniecznych do otrzymania pierwiastka z żądaną dokładnością.

Miarą jakości metody w pobliżu dokładnego pierwiastka może być wskaźnik efektywności

10*