82397

Część 1 15. ZADANIA POWTÓRKA 27

Równanie kanoniczne ma postać:

S„ X,+6,_r=0

Tworzymy wykresy momentów dla: • stanu A'/ = 1

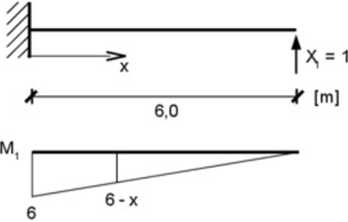
Rys. 15.39. Stan od siły X_t = 1 oraz wykres momentów

• stanu P (pamiętając, źe obciążenie w postaci momentu porusza się po belce (w zależności od.v))

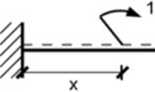
Jh

6.0

* [m]

M_p

x    6- x

Rys. 15.10. Stan odsify P ora: wykres momentów

Korzystając ze wzoni

j s

M, M_t EJ

k

(15.35)

Otrzymujemy:

AlmaMater

Dobra D.. Jamb rożek S.. Komosa M., Mikołajczak E.. Przybylska P.. Sysak A.. Wdowska A.