P3310026 (2)

1- Zagadnienia wstępne

W liczniku, od części zróżnicowania zmiennej A', wyjaśnionej przez zmienne A. i A, i R{ .. i odejmuje się tę część zróżnicowania, którą wyjaśnia tylko zmienna Y.ir. ). Różnicę stanowi dodatkowe zróżnicowanie wyjaśnione przez X,, gdy wcześniej już działa X, Dzielenie tej różnicy przez część zróżnicowania mew v jasnioną przez X, (1 — r.\) daje kwadrat współczynnika korelacji cząstkowej między A . i X, przy kontrolowaniu X₂ (zob. Blalock, 1975).

Wzór i 1 42) uogólniony na większą liczbę zmiennych niezależnych możemy zapisać w postaci

23.. (p—1))

1 p-23...(p—1)

(1- ą²,

1(23. .Cp—I ))

(1.44)

W idzimy zatem, że kwadrat współczynnika korelacji cząstkowej danego rzędu zawsze można interpretować jako iloraz: (zmniejszenie zmienności niewyjaśnionej )/(zmienność poprzednio niewyjaśniona) i zapisywać

przy czym „poprzednie niewyjaśnienie" odnosi się do wymiaru niższego o jeden, przed dołączeniem kolejnej zmiennej. Łatwo napiszemy wzór dla układu czterech zmiennych, wśród których jedna jest wyróżniona jako zmienna zależna

Feżeli operujemy kategorią wyjaśniania zmienności (zmiennej wyróżnionej przez zmienne pozostałe), to kwadrat współczynnika korelacji cząstkowej można nazywać współczynnikiem cząstkowej determinacji.

Przykład 1.4. (statystyka środowiska)

Powracając do naszego problemu korelacji poboru wód podziemnych (A',) i emisji pyłów [X₂) oraz pośredniczącego wpływu liczby ludności (X,) i liczby zakładów uciążliwych dla czystości powietrza (X₄), wyznaczymy ze wzoru (1.39) kwadrat współczynnika korelacji wielorakiej

0778² + 0764² - 2 • 0778 • 0,764 • 0,838 1-0,838¹

*0,647

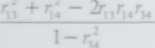
a następnie

R,

=    = 0,804

który informuje o silnym skorelowaniu ilości pobieranych w od podz.iemnychl z liczbą ludności i zakładów uciążliwych razem wziętych. Oznacza lo, żc te d\\ u