P1111272

50

C6*)

VIII. Funkcja pierwotna (całka nieoznaczona)

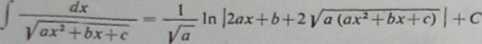
= —~ln \ax+\b+ j/o (ax²+bx+c) I+C',

1/st    »    ^

a dla a<0

(7*)

dx    1

----arc sin

}/ox²+bx+c    j/joT

2ax+b tfb*—4ac

6) Zajmiemy się teraz podstawieniami Eulera. W ustępie 269, 12) zastosowaliśmy właściwie pierw, sze podstawienie do obliczenia całki

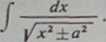
Chociaż drugą całkę podstawową

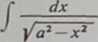
znamy już z rozważań elementarnych, jednak jako ćwiczenie zastosujemy do niej podstawienie Eulera, (a) Jeśli zastosujemy najpierw trzecie podstawienie ya²—x* = / (a—x), to otrzymamy

oraz

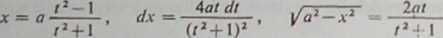
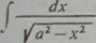
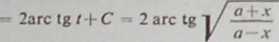
Ponieważ zachodzi tożsamość

2 arc tg    -- arc sin — + —    (—a < x < a),

Y a—x    a 2

więc wynik ten różni się tylko kształtem od znanego nam już wyniku.

Czytelnik powinien dalej też liczyć się z możliwością otrzymywania różnych form tej samej całki w zależności od metody zastosowanej do jej obliczania.

a²—x² — xt—a, otrzymamy analogicznie

(b) Jeśli zastosujemy do tej całki drugie podstawienie }/i

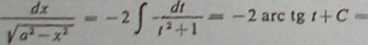
-2arct _s°±j£EŻE-_+C.

X

Napotykamy tu inną ciekawą osobliwość ('): wynik ten jest poprawny osobno dla przedziału (—a, 0) i osobno dla przedziału (0, a), w punkcie x ---• 0 bowiem wyrażenie

X

2arc „£±j5EZ

pozbawione jest sensu. Granice tego wyrażenia przy x-+-0 I przy x->+0 są różne, równają się one odpo* wiednio ri -n. Wybierając dla wspomnianych przedziałów różne wartości stałpj C tak, by druga wartość była większa od pierwszej o 2n, możemy zestawić funkcję ciągłą w całym przedziale (-a, a), jeśli przyjąć jako jej wartość dla * — 0 wspólną granicę lewostronną i prawostronną.

(^ł) Por. na przykład [)) 277).

§ 3. Całkowanie pewnych wyrażeń zawierających pierwiastki

51

1 tym razem otrzymaliśmy poprzedni wynik tylko w innej formie, ponieważ zachod/ą tożsamości

—2arc

,g 5+jGEZ.-

arc sin—--n    dla 0 < x< a.

a

arc sin — +n dla -a < x < 0. a

⁷⁾J

dx

jc+i/jc¹—JC-ł-1

(a) Zastosujemy najpierw pierwsze podstawienie —jr+T = t—x\ otrzymamy

ITT* ^d    (2i-iT*'

r_&--r**-²'-?*. rfi—ł—+—j—1*

J x+Yxⁱ-JC+1    ^J I(2/— l)^a    J 1/ 2/-1    (2(~l)^ł J

- - 4 * T^-T +^2,n I'I-T->" PMll+C..

2 2/—1 2

Jeżeli podstawimy tu t = x+|A*^ł—*+1, to otrzymamy ostatecznie

f    _m _ 2. _1__

‘ jt+^jc^-jc+l    ²    2jc-ł-2|^jc*—jc4- 1 — 1

— y21n |2x+2j/x²—jr+l —1| +2 In lx+/P^T7T| + C.

(b) Zastosujemy teraz drugie podstawienie: ^x^l—x+1— tx— 1, mamy

*

-2'-'^+'rf/, (f^2-l)^J		—— r-i*ft -x+i - (1_1	, i — JL. /-I
( — 2/^2 H- 2/ — 2		i* r 2 i.i	3 1	) i
		J li 2 / I	2 r+l	(/+!)* J

iż

—ł_r+2ln|f|-~lⁿ)r— 11 ——*!r» |/ H| ł-C\ /+! 2 2

..    |/jr*—jr-ł-111 .

IC t » .......— i po ocz

12 lo 1/7*^771 >l|

Pozostaje teraz podstawić t — ^r-'~ ■    ..1.1-1 j po oczywistych uprot/c/cnuch otrzymujemy

3x

C dx

c+^x^ł-x+l ]/xⁱ-x+\+x+l

“■ln||fx^ł - % ♦ 1- ł-f l| j tnjyCs* z i I ! i . tj •. c

Wyrażenie to chociaż różni sią kształtem od otrzymanego wyżej, jednak pokrywa wg t tum, ab C'-C+ 4