PA274997

ANALIZA STATYSTYCZNA DANYCH

Litery możemy wybierać dowolnie, posługując się inicjałami przyjaciół i znajomych, choć zwykłe zaczyna się od pierwszej litery alfabetu. Tabela testu S-N-Kjst wygodna do nadania indeksów', bo każda kolumna tej tabeli to inny indeks. W tabeli testu Bonferroniego jest to trochę trudniejsze. Tabela 9.2 zawiera przykładowy sposób indeksowania średnich.

Tabela 9.2. Sposób indeksowania średnich w testach post hoc

Typ wiadomości poprzedzającej reklamę	Relacja z konfliktu zbrojnego	Relacja z parlamentu	Relacja z tańca
Procentowy wzrost sprzedaży	23.9a	15,6b	33,4C

Przykładowy raport

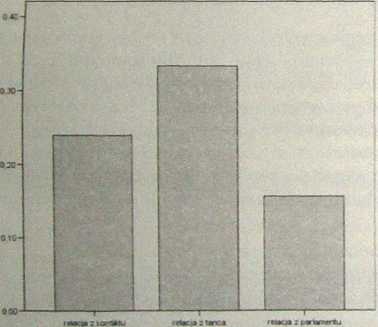
W celu przetestowania hipotezy o wpływie informacji o różnym nasyceniu emocjonalnym (operaęjonalizaąja: trzy typy wiadomości) na skuteczność reklamy (ope-racjon&lizacja: procentowy wzrost sprzedaży reklamowanego towaru - zmienna na skali ilościowej) przeprowadzono jednoczynnikową analizę wariancji w planie dla grup niezależnych. W wyniku tych analiz uzyskano istotny statystycznie efekt zmiennej rodzaj wiadomości, F(2, 57) = 23,83; p < 0,001 (por. rys. 9.14). Przeprowadzone porównania post hoc za pomocą testu Scheffe ujawniły istotne różnice (p < 0,01) między wszystkimi grupami.

Yfykres średnich (patrz rys. 9.14) pokazuje, że najwyższy wzrost sprzedaży reklamowanego towaru wystąpił w regionie, gdzie przed reklamą pokazywana byia pozytywnie nacechowana wiadomość (M = 0,33; SD = 0,09), mniejszy tam, gdzie

średnia skut

wtad

Rys. 9.14. Procentowy wzrost sprzedaży reklamowanego produktu w zależności od typ^u telewizyjnej poprzedzającej reklamę.

9 • JEDNOCZYNNIKOWA ANALIZA WARIANCJI...

pokazywano negatywnie nacechowaną relację z konfliktu (M * 0.24; SD ~ 0,07), a najmniejszy tam, gdzie relacja z obrad parlamentu poprzedzała reklamę (Jf = 0,16; SD = 0,07).

Język poleceń

Wykonanie jednoczynnikowej analizy wariancji w edytorze poleceń jest niezwykle proste. Wystarczy podać komendę ONEWAY oraz listę zmiennych. W naszym przykładzie będzie wyglądać to następująco:

ONEWAY

skut BY wiad    — lista zmiennych

/STATISTICS DESCRIPTIVES    - statystyki opisowe

/PLOT MEANS.    — wykres średnich

/POSTHOC = SNK SCHEFFE BONFERRONI ALPHA {. 05) . -rodzaj testu post hoc

Porównania a priori (kontrasty)

W przypadku kiedy wynik testu F jest istotny, analizy post hoc pozwalają sprawdzić, które średnie różnią się od siebie istotnie statystycznie. Porównania post hoc wykonujemy wtedy, kiedy hipotezy są niekierunkowe. Jednakże bardzo często znajdujemy się w sytuacji, w której wiemy na podstawie wcześniejszych badań lub/oraz teorii, że konkretna średnia będzie większa od pozostałych średnich. W naszym przykładzie hipoteza taka mogłaby wskazywać, że obejrzenie relacji z tańca irlandzkiego na tyle poprawi nastrój widzom, że następująca po niej reklama będzie znacznie bardziej skuteczna.

Kiedy mamy tak postawioną hipotezę możemy, niezależnie od wyniku testu F_y wykonać porównania planowane, których układ odzwierciedla postawioną hipotezę. Najpierw ustalamy, które grupy kontrastujemy z którymi. Załóżmy, że chcemy porównać grupę drugą z pozostałymi. A zatem zakładamy, że średnia w drugim warunku eksperymentalnym będzie różna od obu pozostałych traktowanych łącznie.

Do analizy tak postawionego problemu wykorzystamy testy kontrastów, które są rodzajem testów' t dla prób niezależnych. Chcemy przecież porównać de facto dwie średnie, więc wykorzystanie testu t wydaje się być naturalne. Teraz musimy jeszcze wskazać średnie do połączenia oraz przeciwstawiane podgrupy średnich. Temu celowi służą wagi (współczynniki kontrastów'), które są niczym innym jak wartościami liczbowymi dodatnimi i ujemnymi.

Przypisując średnim wagi posługujemy się określonymi zasadami. Przede wszystkim musimy ustalić tyle wag, ile poziomów ma czynnik (tyle ile jest grup w badaniu). Podgrupy średnich, które chcemy ze sobą skontrastować, powinny mieć przypisane współczynniki kontrastu o przeciwnych znakach.

Porównania a priori (kontrasty)

Porównania

planowane

Testy kontrastów

Współczynniki

kontrastów