PA274999

ANALIZA STATYSTYCZNA DANYCH

ności jest bardzo ważny. Pamiętajmy, że możemy wykonać wyłącznie tyle porów-nań, ile jest grup badawczych minus jeden.

Przypisanie wag dla drugiego kontrastu nie powinno już stanowić większej trudności. Przypomnijmy, że chcemy porównać grupy I i 3. Wagi kontrastu mogą mieć takie wartości jak w tab. 9.5. Tak wykonana tabela wag w testach kontrastów, jeszcze przed przypisaniem wag w SPSS, jest nieocenioną pomocą dla badacza. Nie tylko w sposób klarowny pokazuje ona, jakie porównania chcemy wykonać, ale również z łatwością możemy sprawdzić, czy są one niezależne, sprawdzając sumę iloczynów odpowiednich wag. Jak ją obliczamy? Otóż najpierw mnożymy przez siebie wagi przypisane w obu kontrastach grupie pierwszej. Jeśli wykonamy tę operację dla wszystkich par współczynników, to sumujemy uzyskane iloczyny, jeśli suma iloczynów wag wynosi 0 (zero), oznacza to, że zaplanowane kontrasty są od siebie niezależne.

Tabela 9.5. Przykładowe wagi dwóch ortogonalnych kontrastów.

Waga	Grupa 1	Grupa 2	Grupa 3	Suma
Kontrast 1	-1	+2	-1	(-1) + 2+(-1)=0
Kontrast 2	-1	0	+1	(-1) + 0 + 1=0
Iloczyn wag	K-1)X(-1)]=1	2x0 = 0	l(-1)x(+1)] = -1 - •; 8	UO+(-1)»0

Gdy chcemy przeprowadzić jednocześnie analizę dwóch kontrastów po zadeklarowaniu wag pierwszego kontrastu, w oknie kontrastów klikamy na przycisk NASTĘPNY i wpisujemy wagi dla kontrastu drugiego (patrz: rys. 9.17). Napis KONTRAST 2 z 2 wskazuje, który kontrast właśnie definiujemy. Gdy klikniemy przycisk POPRZEDNI, zobaczymy współczynniki poprzednio wpisanego porównania.

Jednoczynnikowa ANQVA: Kontrasty		W
f“ WWonian pf|
	fe h m i d	Oafcf {
		Anki |
| Poprzedni | | Następny J j		Ponoć |
1 Współczynniki: In *i£±j, i mi
	-ł 0 1
; Suma wgpćtczynrików. 0.000

jjednoczynrakołia ANOVA: Kontrasty    . - - ■ ijjBfj

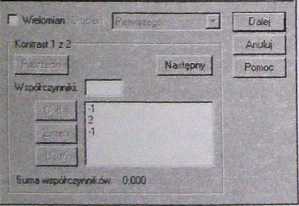
Rys. 9.17. Definiowanie drugiego kontrastu.

Wydruk wyników, jaki otrzymamy w SPSS, jest bardzo pomocny i czytelny. Po pierwsze, dostajemy tabelę prezentującą wagi obu kontrastów co pozwala skontrolować poprawność wprowadzenia wag (patrz: rys. 9.18). Jeśli zrobiliśmy to poprawnie, to tabela ta powinna być identyczna z tą, którą stworzyliśmy planując porównania a priori (tab. 9.5).

9 • JEDNOCZYNNIKOWA ANALIZA WARIANCJI..-

Współczynniki Końti a stu

Kontrast	wiad
	relacja z konfliktu	relacja z tańca	relacja z parlamentu
^1	-l •1	0	-1

Rys. 9.18. Tabela prezentująca WSPÓŁCZYNNIKI KONTRASTU.

W kolejnej tabeli zawarte są statystyki obu testów kontrastów (patrz m, 9.19). Ponownie czytamy wyniki z pierwszej części tabeli Założono równość wariancji i interpretujemy je identycznie jak powyżej.

Wykonane kontrasty oznaczone są numerami 1 i 2. W tabeli na rys. 9.19 Widzimy, że wynik pierwszego kontrastu jest następujący*. f(57) = 6,09; p < 0,001, a kontrastu drugiego /(57) = 3,24; p < 0,01. Oba porównania są istotne staty-stycznie.

Testy kontrastu

Kontrast	Wartość kontrastu	Błąd standardowy	t	dr	Motoete (dwuslrema)
skut Założenie o I	.2715	.04456	6,093	57	.880
równości wariancji 2	-.0835	,02573	-3,245	57	.002
Brak założenia 0 1 równości wariancji 2 ’	,2715	.04765	5.698	31,971	m
	-.0835	.02381	-3,507	37,919	,001

Rys. 9.19. Wyniki dwóch testów kontrastów.

Opis wyników może wyglądać następująco:

Aby odpowiedzieć na pytania kierunkowe, przeprowadzono w analizie wariancji porównania planowane. Pierwsze porównanie kontrastowało procentowy wzrost sprzedaży po relacji z tańca irlandzkiego z pozostałymi grupami. Porównanie to okazało się istotne statystycznie £(57) = 6,09; p < 0,001 - średni wzrost sprzedaży po relacji z tańca był wyższy (M = 33%) niż w pozostałych grupach (80%). Drugie porównanie kontrastowało skuteczność reklamy nadawanej po relaęji z parlamentu i po relacji z konfliktu zbrojnego. Analiza kontrastu wskazała istotne różnice między dwiema średnimi £(57) = 3,24; p < 0,01. Wzrost sprzedaży po relacji z parlamentu był niższy (M = 15,6%) niż po reklamie z konfliktu zbrojnego (M - 84%).

Język poleceń

Wprowadzone kontrasty można wykonać za pomocą następujących poleceń:

ONEWAY    - nazwa analizy

skut BY wiad    - nazwa zmiennej zależnej/nazwa czynnika

/CONTRAST= -1 2 -1 /CONTRAST= -10 1. - współczynniki kontrastów