PC043351

Rozdział 3. Funkcje jednej zmiennej

Uwaga. W przypadku, gdy q = f, twierdzenie nie rozstrzyga problemu. Przykład 3.21.

Za pomocą kryterium d’Aiemberta zbadamy zbieżność wybranych szeregów, a) Niech aę R będzie ustaloną liczbą. Dla szeregu pUj ^ mamy

Szereg jest więc zbieżny dla każdego a. b) Dla szeregu £", mamy

«*b+i    y^+,(n + l)!n"    3    3

co oznacza, że szereg jest rozbieżny.

Twierdzenie 3.14. (Kryterium Cauchy’ego)

Zafdżmy, że dla szeregu a„ istnieje granica r = lim Vi<żj- Wtedy:

a)    jeśli r < 1, to szereg jest zbieżny,

b)    jeśli r > 1, to szereg jest rozbieżny.

Uwaga. W przypadku, gdy r = 1, twierdzenie nie rozstrzyga problemu. Przykład 3.22.

Zastosujmy kryterium Cauchy’ego do zbadania zbieżności wybranych szeregów, a) Dla szeregu , ff mamy

szereg jest więc zbieżny dla każdego a. b) W przypadku szeregu:    (l + |) mamy

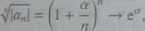
gdy n —» oo.

Szereg jest więc zbieżny dla ar < 0, rozbieżny dla ar > 0. Dla a = 0 rozważa kryterium nie rozstrzyga problemu, widać jednak, że wyrazy szeregu byłyby róws 1 i tym samym szereg byłby rozbieżny.

Definicja 3.9.

Niech (a„) będzie ciągiem liczb jednakowego znaku. Szeregiem przemiennym nazywamy szereg

00

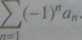
(3.7)

3.3. Funkcje. Granica i ciągłość

Twierdzenie 3.15. (Kryteriom Leibniza)

Jeśli ciąg (a„) jest monofoniczny i zbieżny do 0, to szereg (3.7) jest zbieżny. Przykład 3.23.

W przypadku tzw. szeregu antaarmonicznego ~ mamy a„ = - - są zatem spełnione założenia ostatniego twierdzenia. Szereg jest więc zbieżny.

Definicja 3.10.

Szereg a_n nazywamy.

a)    bezwzględnie zbieżnym, jeżeli szereg £_n l^flnl jest zbieżny,

b)    warunkowo zbieżnym, jeżeli jest on zbieżny, lecz nie jest bezwzględnie

zbieżny.

Przykład 3.24.

Z rozważań przykładów 3.19 oraz 3.23 wynika; że szereg anharmoniczny jest zbieżny warunkowo.

Twierdzenie 3.16.

Jeżeli szereg jest zbieżny bezwzględnie, to jest zbieżny.

3.3. Funkcje. Granica i ciągłość 33.1. Granice funkcji Definicja 3.11.

Punkt xo € R nazywamy punktem skupienia zbioru A c R wtedy i tylko wtedy, gdy istnieje ciąg o wyrazach należących do zbioru A - Uol i zbieżny do ób*

Punkt xo e A, który nie jest punktem skupienia zbioru A nazywamy punktem izolowanym tego zbioru.

Mówimy, że zbiór A ma punkt skupienia w oo (-co) wtedy i tylko wtedy, gdy istnieje ciąg (jc_n) elementów tego zbioru dążący do oo (-oo).

Przykład 3.25.

Wszystkie punkty zbioru A = (£: n e N) są izolowane. Jedynym punktem skupienia A jest 0.

Zbiór liczb wymiernych i zbiór liczb niewymiernych nie mają punktów izolowanych. W obu przypadkach zbiorem punktów skupienia jest zbiór liczb rzeczywistych.

Definicja 3.12. (Definicja Heinego granicy funkcji w punkcie) Niech xo będzie punktem skupienia zbioru X c R. Mówimy, że funkcja f : X —* R ma w punkcie xq granicę ar, co zapisujemy Hm /(x) = ar, wtedy

i tylko wtedy, gdy dla każdego ciągu (x„) o wyrazach należących do i zbieżnego do xo zachodzi

(3.8)

lim f(x_n} - a.

m