PC043352

Rozdział 3. Funkcje jednej zmiennej

Uwagi.

a)    Definicja 3.12 obejmuje także przypadki a = ±co.

b)    Jeśli zbiór X ma punkt skupienia w oo, to podstawiając w definicji 3 J xo = 00 otrzymujemy określenie granicy funkcji w nieskończoności;

Hm f(x) = a <=> A (x_n e X, x_n —+ 00    f(x„) —* a).

X    '    '

(x»)

Analogicznie definiujemy granicę funkcji w —00.

c)    Zakładając, że wszystkie wyrazy ciągu (*„) są mniejsze (większe) od* otrzymamy definicję granicy lewostronnej (prawostronnej) funkcji / w punkcie xq. Granice te będziemy oznaczali, odpowiednio, przez

lim /(ar), lim f(x).

Twierdzenie 3.17.

Jeżeli funkcje /, g mają skończone granice w punkcie xo, równe odpowiednio a, fi. tor.

a)    Km (/(or> + g(x)) = a +/?,

b)    lim (/(or)g(x)> = afj,

c ł lim    o ile / 0 i g(x) / 0.

g<X) >5

Powyższe wzory zachodzą także dla granic jednostronnych.

Przykład 3.26.

a)    Obliczymy granicę funkcji /(jr) = w punkcie -r₀ = 1 - Załóżmy, że (x„) jea dowolnym ciągiem o wyrazach różnych od 1 i zbieżnym do I. Ciąg wartości funkcji

/(jew) =    =■ *» + 1 ma zawsze granicę 2, niezależnie od wyboru konkretnego

ciągu Cr,). Stąd lim f(x) = 2.

b)    Granica lim j nie istnieje. Istotnie, rozważając ciągi x_n = £ oraz y„ = - j. gdzie n € 2V, widać iż ciągi wartości funkcji (^-) oraz (—) dążą, odpowiednio, do 00 oraz ■ -00. Mają więc różne granice. Istnieją natomiast granice jednostronne lim j =

Km i aoo.

x—Qr *

Definicja 3.13.

Prostą o równaniu y = ax+b nazywamy asymptotą ukośną wykresu funkcji / w —00 wtedy i tylko wtedy, gdy

(3.9)

lim (/(z) — ax — b) = 0.

M > 09

Jeżeli a = O, to asymptotę nazywamy poziomą. Zamieniając we wzorze (3.9) granicę w — oo na oo, otrzymamy określenie asymptoty w oo. Prostą o równaniu x — c nazywamy asymptotą pionową lewostronną wykresu funkcji / wtedy i tylko wtedy, gdy

lim /(*) = oo lub lim /(*) = —oo.

x—*c~    jc-nr

Zmieniając granicę na prawostronną, otrzymujemy określenie asymptoty pionowej prawostronnej. Prostą, która jest zarazem asymptotą lewo- i prawostronną, nazywamy asymptotą obustronną (dwustronną).

O tym, czy prosta x — c jest asymptotą wykresu funkcji decydują wartości tej funkcji w sąsiedztwie punktu c. Wartość f(c) (jeśli jest określona) nie odgrywa natomiast żadnej roli. Przykładowo prosta o równaniu x = 0 jest asymptotą pionową wykresu każdej z funkcji

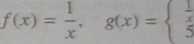
dla x # 0, dla x = 0.

0 asymptocie w -oo (w oo) mówimy często, że jest lewostronna (prawostronna). Twierdzenie 3.18.

Prosta y = ax + b jest asymptotą wykresu / w -co wtedy i tylko wtedy, gdy liczby a,b są równe

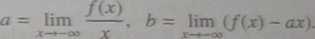
(310)

Analogiczne wzory zachodzą dla asymptoty ukośnej w oo.

Przykład 3.27.

a) Wykres funkcji f(x) =    , x € R — (Oj, ma asymptotę pionową (dwustronną)

o równaniu x = 0, bowiem

Um /(*) = -oo, lim f(x) = oo. *—O-    jc—O*

Ponadto f(x) = x - 2 + a stąd

lim (/(*) - (x - 2» = 0.

Prosta o równaniu y — x — 2 jest więc asymptotą ukośną dwustronną wykresu /. b) Prosta y = * nie jest asymptotą funkcji /(*) = * + sin*. Granica lim (/<j> - _n

nie istnieje, nie równa się więc w szczególności 0. Zauważmy, że w przypadku rozważanej funkcji nie istnieją żadne asymptoty.

11S