PC043361

Rozdział 3. Funkcje jednej zmiennej

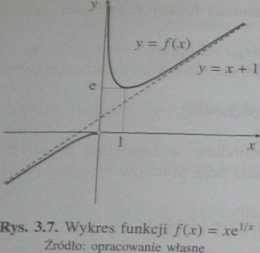
W =

3.43. Zastosowanie pochodnych w ekonomii

Wprost z definicji pochodnej (definicja 3.15) wynika, że dla wartości h jifl bliskich 0 mamy

_y -lim^/(Xo'^>~*⁾~^/C*^o) 1 /(to + W-fM ^{J h}~^¥°    h    I    A

Zakładając, że wartości funkcji „nie zmieniają się zbyt szybko”, możom podstawić h = 1> otrzymując

/'(*o) - /C*0 + 1) -/(*o).

Wartość f'(xo) jest więc w przybliżeniu równa przyrostowi wartości funkcji i w przypadku, gdy wartość argumentu wzrośnie o jednostkę (licząc od poczat- j kowej wartości ,ro). Wartość /'(*o) może być uznana za miarę szybkości zmian ; wartości funkcji

Przykład 3.49.

Niech x oznacza wielkość produkcji w pewnym przedsiębiorstwie, a AT(x) —jej caftonih¹ | koszt Wówczas funkcję K' (o ile istnieje) nazywamy funkcją kosztów krańcowych.

Załóżmy, że funkcja kosztów ma postać K(x) = 0,2r² + 6x + 200, x > 0. Wtedy [ kT'(jc) = 0.4.r + 6 i w szczególności AT'(10) = 10 oznacza przybliżony wzrost kosztów j w przypadku, gdy wielkość produkcji wzrośnie z poziomu 10 do 11. Dokładna wtok jest równa 25f(l 1) — K(10) = 10,2.

Definicja 3.20.

Współczynnikiem elastyczności funkcji / w punkcie xq nazywamy liczb? (o ile istnieje)

xpf'(xo) /(•*&)

Bastyczność dodatniej funkcji różniczkowainej w punkcie x« > 0 określa przybliżoną względną zmianę wartości funkcji przy zmianie argumentu o 1% (przy początkowej wartości xq). Oznacza to, że jeśli argument wzrośnie o 1%, to wartość funkcji zmieni się w przybliżeniu o E_Xnf%.

Przykład 3.50.

Współczynnik elastyczności funkcji kosztów z przykładu 3.40 w punkcie jco = 10 jest równy około 0.36. Jeżeli więc wielkość produkcji x zwiększymy o 1% (licząc od początkowego poziomu xo = 10), to koszt wzrośnie w przybliżeniu o 0*36%.

Podobne zastosowanie ma pochodna w odniesieniu do innych funkcji wy-[ stępujących w ekonomii. I tak na przykład z funkcji utargu całkowitego można [ uzyskać funkcję utargu krańcowego i przeciętnego, z funkcji produkcji - funkcję [ produkcji krańcowej i przeciętnej itp.

1 3.4.4, Wzór Taylora i wzór Maclaurina

Twierdzenie 337. (Wzór Taylora)

leżeli funkcja f jest (n +1 )-krotnie różniczkowalna w sposób ciągły na pewnym pizedziale (a,b), to dla dowolnych x,xq e (a,b) istnieje liczba 9 e (0,1) taka. k

/(*) = /(*)) + —- *o) + - £*\x - J.....*

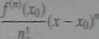
(3.18)

Uwagi.

aj Ostatni składnik po prawej stronie równania (3.18) nazywamy resztą n-tego rzędu (w postaci Lagrange^Ta). Będziemy go oznaczali symbolem R„(x,xq\ Oznaczając J*® = f , wzór Taylora (3.18) można zapisać w postaci

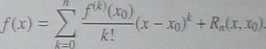
Przyjmując w (3.18) xo = 0, otrzymamy tzw. wzór Maclaurina:

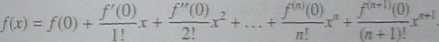
b) Zauważmy, że dla n = 0 wzór Taylora przyjmuje postać f(x) = /(-*o) + f(*o +0(x- xo))(x - xq).