PC043357

Rozdział 3. Funkcje jednej zmiennej

.14.2. Zastopowanie pochodnych do badania przebiegu zmienny funkcji    ¹

Rozważymy jedynie niektóre zastosowania pochodnej, a mianowicie w ota niu grenie, badaniu monotoniczności i wyznaczaniu ekstremów funkcji. -W

Twierdzenie 3.29. (Reguła de l*Hospitala)

Jeśli funkcje / oraz g spełniają warunki:

ą) lim f(x) = ±oo i lim g(x) = ±oo albo lim f(x) = lim g(x) = 0,

' — M'    x—»xo    a-*.v₀

bj /. g są różniczkowalne w pewnym sąsiedztwie punktu xq (to znaczy w ^ rze (ao - r, xo + r) - {^} dla pewnego r > 0), e) istnieje granica

X—*Xę

to istnieje granica

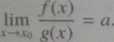
Twierdzenie 3.29 pozostaje prawdziwe również w przypadku granic jednostronnych, dla jęp = ±°° oraz granic niewłaściwych, tj. gdy a = ±co.

Przykład 3.39.

Obliczymy granicę lim Funkcje f(x) == ę^^^(^_=^^_różnięzkoMlnejnn

wyjściowa granica także jest równa 1.

I waga. Założenie c) reguły de 1’Hospitala jest istotne (podobnie jak pozostałej Rozważmy mianowicie granicę

_2 . 1 x sin -

_ X

lim-

x—*o sin x

Łatwo ją wyznaczyć:

Założenie c) reguły de FHospitala nie jest natomiast spełnione, bowiem# |smieje granica ilorazu pochodnych

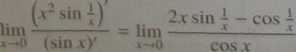
TWIERDZENIE 3.30.

Niech / będzie funkcją różniezkowalną na przedziale (o, b). Wówczas:

a)    funkcja / jest nłemalejąca (nlerosnąca) na przedziale (a, b) wtedy i tylko wtedy, gdy dla każdego x e (a,b) zachodzi nierówność f'(x) > 0 (odpowiednio f\x) < 0),

b)    jeśli dla każdego x e (a, b) zachodzi f'{x) > 0, to / jest funkcją rosnącą nu przedziale (a, b),

c)    jeśli dla każdego x e {a,b) zachodzi f'(x) < 0, to / jest funkcją malejącą na przedziale («, b).

Przykład 3.40.

Wyznaczymy przedziały monotoniczności funkcji f(x) = X⁴-!*², x e if. Mamy f'{x)» 4jc(x - 1)(jc + 1), ,v 6 U i dlatego

/'(jc) < 0 o .r € (-oo,-1) u (0,1), f(x), > 0 » x € (-1,0)U U,co).

Funkcja / jest więc malejąca na każdym z przedziałów: (-<»,-1) oraz (0,1). natomiast rosnąca na każdym z przedziałów: (-1,0) i (l,oo).

Uwagi.

a)    Fakt, iż teza twierdzenia 3.30 dotyczy monotoniczności funkcji na przedziale nie jest przypadkowy. Dla funkcji f(x) = i, x # 0, mamy zawsze /'(*) = —4j- <0 — jest ona malejąca na każdym z przedziałów (—oo, 0) oraz (0,co). Nie jest ona jednak monotoniczna na ich sumie, czyli dziedzinie funkcji.

b)    Zakładając dodatkowo ciągłość funkcji / na końcach przedziału, tezę ostatniego twierdzenia można rozszerzyć na przedział domknięty. Przykładowo, jeśli funkcja / jest ciągła na (a,h) oraz /'(*) > 0 dla * e (a,b), to / jest rosnąca na (a, b).

Definicja 3.17.

Mówimy, że funkcja f: X -* R ma maksimum lokałne w punkcie .ro wtedy i tylko wtedy, gdy

y /\ /taWM-    (3,16)

r>0 Jte(*o-ł\*o+r)nX

Funkcja / ma w punkcie % minimum lokalne wtedy i tylko wtedy, gdy funkcja —f ma w tym punkcie maksimum lokalne.

Minimum i maksimum lokalne funkcji / nazywamy ekstremami lokal* nymi funkcji. Jeśli warunek (3.16) jest spełniony dla każdego r > 0, to mówimy, że funkcja / ma w punkcie -ro maksimum globalne. Wtedy

/\/(*o) >/(*).

xek

Minimum globalne / definiujemy analogicznie.