PICT0017 (22)

lilii i i i i

Jeżeli własności plastyczne blachy są identyczne wc wszystkich kierunkach leżących w płaszczyźnie arkusza, ale różnią się ono od własności w kierunku prostopadłym (normalnym) do powierzchni blachy, to wykazuje ona tzw. anizotropię normalną.

W celu stwierdzenia czy określona blacha ma własności anizotropowe oraz ewentualnie jaki jest rodzaj tej anizotropii, wyznacza się wartości współczynników r dla próbek o osiach tworzących różne kąty o z kierunkiem walcowania (rys. 1.36a), a następnie sporządza się w układzie współrzędnych biegunowych r,a wykres funkcji r(a).

Wyraźna zmiana wartości współczynnika anizotropii r wraz ze zmianą kąta a oznacza, że blacha wykazuje anizotropię płaską. Przypadek ten ilustruje rys. 1.16c, na którym pokazano wykresy dla dwóch blach o różnej anizotropii płaskiej.

Stała wartość r, wyraźnie różna od jedności, wskazuje, że występuje anizotropia normalna blachy. Wykresy biegunowe dla tego rodzaju blach pokazano na rys. 1.16d. Jedna z nich ma współczynnik anizotropii r = 0,9, druga zaś r = 1,4. Jeżeli r z 1, to blacha ma własności izotropowe. Wykres biegunowy dla takiej blachy przedstawia na rys. 1.16d linia przerywana.

Sporządzanie wykresów biegunowych jest pracochłonne. Dlatego też najczęściej poprzestaje się na wyznaczeniu wartości r dla trzech rodzajów próbek, których osie tworzą z kierunkiem walcowania kąty 0°, 45° i 90°. Wyznaczono wartości r₀, r_łS i r_w pozwalają ocenić stopień płaskiej anizotropii badanej blachy oraz służą do określenia wartości średniego współczynnika anizotropii normalnej

Ur =

ro-ł-2r₄₅+r_M

4

(1.35)

1.23. WARUNEK PLASTYCZNOŚCI I PRAWO PŁYNIĘCIA

Warunek plastyczności dla blach poddanych płaskiemu stanowi naprężenia i wykazujących anizotropię normalną można określić równaniem

(l+r)ffp= (l+r)«*—2rc_xo_t-ł-(l+r)ff|,    (1.36)

natomiast prawo płynięcia dla tego rodzaju blach ma postać następującą:

_ifŁ_ ^ie* ^de* _{=    (137)}

(l+r)o_x—ro, (l+r)cra—r<y_x — <r_x— cr₂ ⁼ (l+r)o, ‘

Łatwo sprawdzić, że po podstawieniu do równań (1.36) i (1.37) wartości r = 1 otrzymamy odpowiednio zależności (1.6) i (1.16) słuszne dla materiału o izotropowych własnościach plastycznych. Należy przy tym pamiętać, żc dla płaskiego stanu naprężenia a_m = J(o_x+ o_t).

W układzie współrzędnych a_vo_t równanie (1.36) przedstawia elipsy pląs-tyozności, które pokazano na rys. 1.17. Elipsy te są -wySłużono lub skrócono [ w stosunku do elipsy dla materiału izotropowego, a wielkie ich osie są nachy-f luno do osi ffi pod kątem 45°. Skrócenie wielkiej osi elipsy zachodzi, gdy r < 1,

' wydłużenie natomiast, gdy r >1. Na rysunku 1.17 wykreślono również elipsę plastyczności dla blachy wykazującej anizotropię płaską, określoną współczynnikami r₀ = 1,5 i r_M = 3,5. Wielka oś tej elipsy tworzy z osią o, kąt większy niż 45?, a granice plastyczności próbek blachy wyciętych równolegle i prostopadło do kierunku walcowania są różne.

moftłiOf onizol ropowy

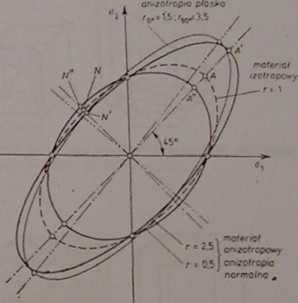
EyB. 1.17. Elipsy plastyczności dla blach o izotropowych i anizotropowych własnościach plastycznyoh

Jak widać z rys. 1.17, występowanie anizotropii normalnej o współczynniku V r > 1 utrudnia przeprowadzenie materiału w stan plastyczny dla stanów naprężenia zbliżonych do dwuosiowego równomiernego rozciągania (punkt #j| ś gdyż wymaga działania większych naprężeń i (<r,)^< niż w przypadku ^materiału izotropowego (punkt A). Jeżeli natomiast oba naprężenia główne Rmają przeciwne znaki (punkt N'), to ten sala materiał wykazuje mniejszy t opór plastyczny niż materiał izotropowy (punkt N). Gdy współczynnik ani-zotropii r<l, wtedy występuje łatwiejszo uplastycznienie materiału przy | dwuosiowym rozciąganiu (punkt A”), a nieco trudniejsze, gdy naprężenia | główno mają znaki przeciwno (punkt N"). f.

13. MECHANIZM ODKSZTAŁCEŃ PLASTYCZNYCH

Wę wszystkich procesach obróbki plastycznej wykorzystuj© się zdolność ^metali do odkształceń trwałych. Jak wiadomo, metale mają budowę krystaliczną, która występuje również po ich odkształoeniu plastycznym. Zachodzi

35

m