ScanImage028

50

Przekształcając pierwszy z tych wzorów i uwzględniając, że dla spoin o przekroju równoramiennego trójkąta prostokątnego a₁=x₁=-^-, otrzymamy:

= V2-X²-^²+3-%²-T?_t

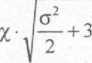
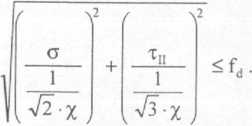
Porównując otrzymane wyrażenie z drugim wzorem, możemy obliczyć współczynniki wytrzymałości spoin pachwinowych:

Oj_ =

V2 •% ’

a„ —

V3-X

Podstawiając wartości liczbowe x [1], otrzymamy:

	X	„ _ ^1 .1 »!=/-V2-x	P II
R9 < 255 MPa	0,7	1,01 (0,9)	0,82 (0.8)
255 < Re < 355	0,85	0,83 (0,8)	0,68 (0,7)
355 < Re < 460	1,0	0,71 (0,7)	0,58 (0,6)

w nawiasie podano wartości z tablicy 18 [1]

Jak stąd widać, w przypadku połączeń teowych są to identyczne wzory, różniące się jedynie w dokładności zaokrąglenia współczynników wytrzymałości spoin cti i och. Jedyna większa różnica (-10%) występuje dla i R_e < 255 MPa.

Przykład 25. Połączenie obciążone siłą poprzeczną i momentem (blacha węzłowa)

Sprawdzić nośność połączenia (rys. 2.12). Stal St3S, R* = 235 MPa, f_d = 215 MPa.

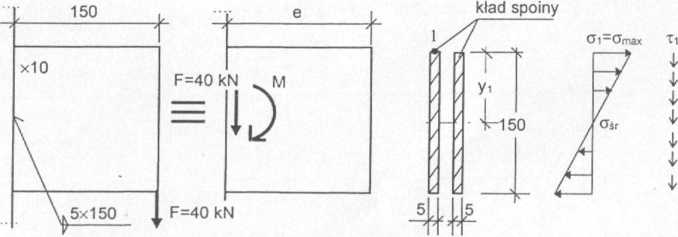
Rys. 2.12

Rozwiązanie

Moment działający na spoinę

M = F • e = 40 • 15 = 600 kNcm. Moment bezwładności kładu spoin

2-ah¹20,515³    ₄

12 12

wskaźnik wytrzymałości kładu spoiny w punkcie 1

W, = -^- =

J_x 281,3

yi ?>5

= 37,5 cnr

_2ah²    2 • 0,5 -15²    ,    ,

W, =---=---= 37,5 cm

lub

6 6

Naprężenie normalne od zginania w punkcie 1

M 600    . .kN

^Gi = —⁼ T7T = 16,0—— = 160 MPa.

W, 37,5 cm

Naprężenia tnące

F 40    kN

^Ti^=-t = T- ⁼ 7-_n. | =2,6-y- = 26 MPa < oCj, ■ f_d = ! 72 MPa A_sp 2 0,5 15 cm

Nośność połączenia. Sposób I

Korzystając ze wzoru

i uwzględniając, że:

otrzymamy

_ '-'i    _

O] t- w + OJ	(i^2 +T^2)<fd
.0 , , o	kN
= = 1I,3-	2 . Ti, - T
2	cm*
^2 +11,3^2	1=16,1 ^kN; =
	cm^2

kN

cm

2 ’

(X = 0,7 dla stali o R* < 255 MPa z tablicy 18 [1]).

Nośność połączenia. Sposób II

Korzystając, wg pkt. 6.3.3.3.C normy [1], ze wzoru

+

)

a

Sfd.

1

uwzględniając, że: