Scan Pic0011

Zadanie 1.57

Aby zwiększyć z/, do/₂ częstotliwość obrotów bryły sztywnej o momencie bezwładności I należy wykonać pracę równą:

Zadanie 1.57

A.

C. i

b.

D. mM

Zadanie 1.58

Dwa jednorodne walce o promieniach .R, = R i 2^ = 2R staczają się bez poślizgu z równi pochyłych o takich samych wysokościach. Stosunek prędkości środków mas tych walców u podstaw równi wyraża się wzorem:

Zadanie 1.59

Punkt materialny wykonuje drgania harmoniczne między punktami A i B (rysu- A    0    B

nek obok), gdzie O jest jego położeniem równowagi. Z A do O punkt ten porusza się ruchem:

A. przyspieszonym    B. opóźnionym

C. jednostajnie przyspieszonym D. jednostajnie opóźnionym

Zadanie 1.60

Ciało wykonuje drgania harmoniczne. W punkcie największego wychylenia z położenia równowagi:

A.    prędkość ciała i jego przyspieszenie są maksymalne

B.    prędkość ciała i jego przyspiesznie są równe zeru

C.    prędkość ciała jest maksymalna, a przyspieszenie równe zeru

D.    prędkość ciała jest równa zeru, a jego przyspieszenie maksymalne

Zadanie 1.61

Jeżeli maksymalna prędkość punktu materialnego wykonującego ruch drgający prosty jest % to w odległości od położenia równowagi równej połowie amplitudy prędkość tego punktu wyniesie:

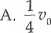
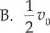
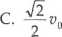
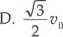
Punkt materialny wykonujący drgania harmoniczne o okresie T jest w chwili t = 0 w maksymalnej odległości od położenia równowagi. Odległość ta zmaleje do połowy w chwili:

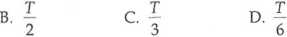
A. T

Zadanie 1.63

Jeżeli maksymalna energia kinetyczna punktu wykonującego drgania harmoniczne wynosi Ep to w odległości od położenia równowagi równej trzem czwartym amplitudy energia ta jest równa:

A.

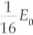
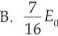
C —E ^C 16 ⁰

D. — E_a 16 ⁰

Zadanie 1.64

Jeżeli ruch cząstki opisany jest równaniem x = Asin—t, to w przedziale T

czasu od 0 do — energia kinetyczna i potencjalna cząstki:

A. rosną I), maleją

C.    kinetyczna rośnie, potencjalna maleje

D,    kinetyczna maleje, potencjalna rośnie

Zadanie 1.65

Zależność całkowitej energii mechanicznej wahadła od amplitudy jego drgań harmonicznych przedstawia wykres:

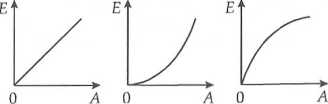
21 -