skan0015 (4)

Wiadomo, że taka funkcja u istnieje wtedy i tylko wtedy, gdy zachodzi warunol

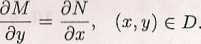
(2&.2J

Gdy warunek (2.5.2) jest spełniony, to równanie (2.5.1) można zapisać ^ postał

du(x,y)?ff 0,

a stąd wynika, że u(x,y) = C jest rozwiązaniem ogólnym równania (2.5.1).

Załóżmy, że równanie (2.5.1) nie jest równaniem zupełnym. W pewnych przq padkach możemy wyznaczyć taką funkcję fi klasy C¹ w obszarze D, że równania

(2.5.3)

fi(x,y)M(x,y)dx + fi(x,y)N(x,y)dy = 0

będzie równaniem zupełnym. Funkcję fi nazywamy wtedy czynnikiem całkującym równania (2.5.1). Zauważmy, że funkcja fi jest czynnikiem całkującym równani!

(2.5.1) wtedy i tylko wtedy, gdy w obszarze D jest spełniony warunek:

d(fiM) ₌ d(fiN) dy dx ’

co prowadzi do następującego związku:

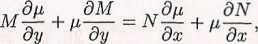
lub po uporządkowaniu

(2.5.4)

Funkcja fi jest czynnikiem całkującym równania (2.5.1), gdy spełnia ona rówl nanie (2.5.4). Rozwiązanie fi równania (2.5.4) jest w ogólnym przypadku trudne do wyznaczenia. Zadanie to upraszcza się, gdy dodatkowo założymy, że poszuki-j wana funkcja fi jest funkcją tylko jednej zmiennej, tzn. zmiennej x lub y. Poniżej] zajmiemy się tymi dwoma przypadkami.

(a) Załóżmy, że fi = fi(x).To oznacza, że fi_y = 0 i równanie (2.5.4) przyjmie postać!

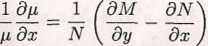
(2.5.5)

Jeżeli wyrażenie po prawej stronie równania (2.5.5) jest funkcją tylko zmiennej x, to czynnik całkujący ma postać:

(li) /ułóżmy, źn /.i ■ //,('//). W lody /i_x ■ 0 1 równanie (2.5.4) przyjmie postać:

(2.5.6)

¹ - _J_ (— -

/idy M \ dy dx)

, In/,nil wy mżenie po prawej stronie równania (2.5.6) jest funkcją tylko zmiennej //, to czynnik całkujący ma postać:

fi(x) = e>f gdzie

1 (dM dN\ ^B^ ~ M\dy dx)'

(t‘) Można też szukać czynnika całkującego w postaci fi(x,y) = x^py^g, gdzie stałe ;> I q należy wyznaczyć. W tym przypadku nie będziemy wypisywać ogólnego wzoru; w rozwiązaniach pokażemy praktycznie, jak postępować, aby taki czynnik całkujący wyznaczyć. Może sie okazać, że równanie różniczkowe może mieć winie czynników całkujących.

Wyznaczyć całkę ogólną równania różniczkowego:

1. (y cosx — x²)dx + (y + sin x)dy = 0

H om wiązanie

ł Mprawdzamy warunek (2.5.2). Ponieważ

dM dN 1 dM dN

-r— = COS a:, %- = cos ®, czyli -5— = -r—

dy dx dy dx

W calnj płaszczyźnie, a więc jest to równanie zupełne. Ponadto wiemy, że

— = y cos® - x , — = y + sin®.

dx dy

^!*Ukując drugie równanie względem y, otrzymamy

u= — +ysinx + ip(x).