skan0025 (3)

28 Stany skupienia materii

(2.22)

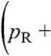
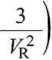
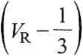
Analogicznie można wyprowadzić zredukowane równanie Berthelota

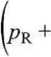
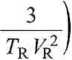
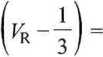
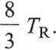
(2.23)

Przykład 2.5. Obliczyć stałe A i B równania Berthelota dla argonu. Objętość i temperatura krytyczna argonu wynoszą, odpowiednio, V_c = 75,2 cm³ • mol^-1 oraz T_c = 150,7 K.

Rozwiązanie. Dla 1 mola gazu równanie Berthelota (2.19) przyjmuje postać

(p + yp_rj(F-B) = RT.    (2.19a)

W punkcie krytycznym, który jest punktem przegięcia na izotermie p =/(kj, muszą być spełnione równania

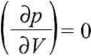
oraz

d²p

dV²

= 0.

T

Ponieważ

(2.19b)

RT A V-B ~ TV² ’

więc

/ dp\ __ RT 2A_    /a²^\ _ 2RT    6A

\dv)_T~ (V-Bf ⁺ TV³ ’    \dV²/T~ (V-B)³    TV^Ą '

W punkcie krytycznym V = V_c, T = T_c, a także

_ RT ₊ 2 A _    2 RT _ 6A _

(V-B)² + TV³ ’    (V-B)³    TV⁴ ~°’

skąd

« = :U. A = %RĘT?.

Po wstawieniu tych wartości do równania (2.19b) otrzymamy, podobnie jak dla gazu Van der Waalsa,

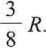
PcK

T_c