skan0021 (5)

24 Stany skupienia materii

Przykład 2.3. Dla jednoatomowego gazu idealnego

_{=    =} AJL A

^K C_v i,R 3 '

Obliczyć, jak zmieni się objętość 1 mola tego gazu w procesie odwracalnego rozprężania od ciśnienia 2,000 barów do ciśnienia 1,000 bara: a) w stałej temperaturze 300,7 K, b) w sposób adiabatyczny. Jaka będzie końcowa temperatura gazu po rozprężeniu adiabatycznym?

Rozwiązanie.

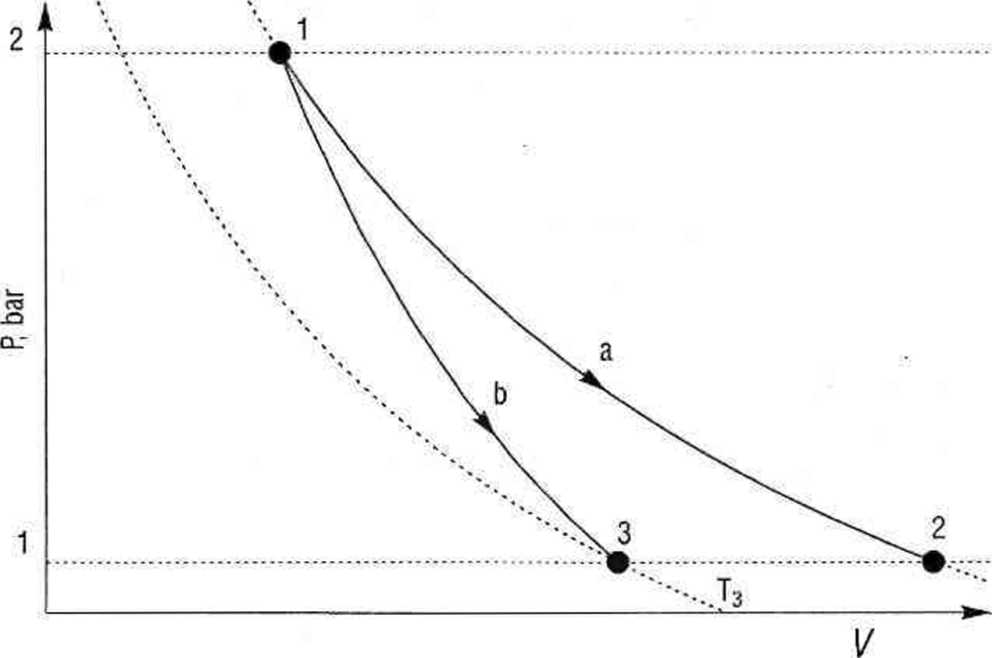
Rys. 2.1. a) izotenna, b) adiabata

a) Proces izotermiczny w T_x = 300,7 K. Zgodnie z równaniem (2.8) mamy

K, _    8.314- 300,7 . ^_m3t

P1

2 • 10⁵

RT_X 8,314-300,7    ,    ,

1 • 10⁵

V, = -- = ’ . -Zr* = 2,500 • 10~² m³.

P 2

b) Odwracalny proces adiabatyczny. Przekształcając równanie adiabaty (2.11), mamy

P i V\ ⁼ p ₂ v$.

Otrzymujemy więc

V₃

Pi

P\

Mk

V,

Pi V\ \P2