skanowanie0001 (169)

6. WYZNACZANIE ELIPSOIDY BEZWŁADNOŚCI CIAŁA SZTYWNEGO

Tensor momentu bezwładności ciała sztywnego

Rozważmy przypadek ruchu obrotowego ciała sztywnego wokjfl osi przechodzącej przez jego środek masy. Ruch ten opis/mny w kartezjańskim układzie współrzędnych, którego początuk pokrywa się ze środkiem masy ciała. Ogólne wyrażenie na mama im pędu ciała sztywnego (a także dowolnego rozkładu dyskretnogo mas) względem wybranego punktu (początku układu współrzędnych)! ma postać:

(6.:i|

gdzie r_t - wektor określający położenie elementu o masie ifl| (całe ciało dzielimy myślowo na elementy traktowane jako punkty

materialne), v - prędkość tego elementu.

Dla ciągłego rozkładu masy wyrażenie (6.1) zapisujemy najczęściej w następującej formie:

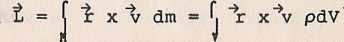
(6.2)

gdzie p - gęstość masy ciała, V, M - objętość i masa ciała.

Ponieważ

la x ||| , (gdzie "ta jest prędkością kątową

ciała), w równaniu (6.1) występuje podwójny iloczyn wektorowy, który można przedstawić za pomocą dwóch iloczynów skalarnych

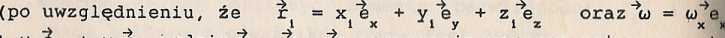
+ ta e +ue, gazie e , e , e oznaczają wersory osi x, y, z) :

Hi,}

(6.3)

f. - >: m₍ ( t) i'! - \ ( 1e] %) ].

(«• I) nkIndowy woktora £ w kierunku osi x zapisujemy

(6.4)

2    A

li "W E m, r, - Em, x, ( r, u>)

x    x    11    i i ' i ¹

, f*» -■ x. <*)    + y w + z w

•    i x i y iz

1 W U', i ? - w Z m xf - u E m, x, y, - u Z m X z .    (6.5)

¹    1    x 1    1    y l 11,, z 1 ; 1 i    '

iMMiUmy oznaczenia:

• *    n,^- x*>    •-    i    , .    (6.6)

‘ ^Z "¹lⁱl^Y(    ⁼    •    <⁶’⁷>

- t m x z    =    I    .    (6.8)

^......... I I I (zwane składowymi tensora momentu

Kx^xyjXZ    i    i ' **>“* [ n^v    ■ ^    . i    u, - - , „„

ludności - wyjaśnienie pojęcia niżej)    zależą od rozkładu

w ciule. Biorąc za przykład wyrażenie:

■„ ■ ^s »,'.<< - ^s «, <1? + *?) («•») Imy, że jest ono sumą iloczynów mas przez kwadraty

IflOŚCl od osi x, a więc rzeczywiście oznacza moment Indności względem tej osi. Dla układu odniesienia ^nie •fltiogo z obracającym się ciałem (w układzie laboratoryjnym)

• i>iwo te zależą od chwilowej orientacji ciała względem osi ilu współrzędnych, a więc^śą Należne" ód cżasu^--Postępując’ Imi n ze składowymi^E^i^X'^ iirożemy ślcładówe ^vwektora momentu Knpisać następująco^