Strona0271

271

Niech na skutek działania przypadkowych zaburzeń początkowych układ wykonuje drgania swobodne z częstością Wówczas czynnik zewnętrzny, zmieniając parametr układu, może w pewnych warunkach doprowadzać okresowo energię do drgającego układu i w tym przypadku amplituda drgań będzie stale wzrastać z czasem. Wystąpi wówczas tzw. rezonans parametryczny.

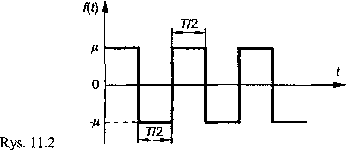
Oczywiście, aby energia dopływała do układu, musi wystąpić odpowiednie dopasowanie częstości zmian parametru do częstości coq. W przeciwnym razie okresowe zmiany parametru mogą spowodować wytłumienie drgań lub te drgania zachowują stałą początkową amplitudę. Aby zanalizować zjawisko rezonansu parametrycznego, przyjęto, że funkcja/^/) ma okres

T

2k

co

(11.6)

oraz postać pokazaną na rys. 11.2, przy czym b < 1. Przyjmując taką szczególną postać funkcji f{t), możemy uprościć w sposób zasadniczy obliczenia, zachowując jednocześnie jakościowy charakter rozpatrywanego zjawiska.

Na początku należy zwrócić uwagę, że - jak wynika z ogólnej teorii równania (11.5) z okresowym zmiennym parametrem - rozwiązania szczególne tego równania mają postać:

e^Mu{t)    (11.7)

gdzie u{i) jest okresową funkcją o okresie T równym okresowi funkcji/(/), stała zaś A nazywa się charakterystycznym wykładnikiem równania (11.5).

Z rozwiązania (11.7) wynika, że w ciągu okresu T funkcja x zmienia się

0    stalą wartość

x(t + T) - e^xrx{t) = cx(0    (11.8)

Oczywiście, jeśli jej > 1, to drgania będą wzrastać nieograniczenie z czasem

1    wystąpi rezonans parametryczny.