26786 img055 (6)

METODY ANALITYCZNEGO PRZEDSTAWIANIA SYGNAŁÓW Uogólniony szereg Fouriera

•    uogólniony szereg Fouriera posiada bardzo istotną, przedstawioną dalej, właściwość

•    dla sygnału x(t) wprowadzimy skończenie wymiarową aproksymację w postaci

gdzie:

w,(r)    - wybrany układ funkcji ortogonalnych (funkcje bazowe)

c, - współczynniki rozwinięcia

• powyższy szereg zapewnia najlepszą aproksymację w sensie minimum błędu średniokwadratowego, jeżeli współczynniki c_j zostaną wyznaczone według wzoru

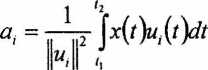
21

METODY ANALITYCZNEGO PRZEDSTAWIANIA SYGNAŁÓW Uogólniony szereg Fouriera

• zatem błąd średniokwadratowy

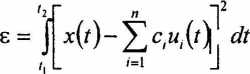
osiągnie minimum, jeżeli c_i = a_t

zakładając, że c, = a_t + b_t, błąd średniokwadratowy aproksymacji wynosi

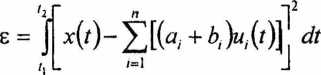
uwzględniając ortogonalność układu funkcji w,.(r), po wykonaniu

nieskomplikowanych przekształceń algebraicznych, błąd średniokwadratowy wyrazimy następująco

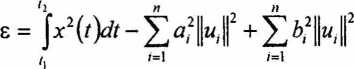
22