27079 img430 (2)

PRZYKIAD 10.

Wyznaczmy lim (x + sin x).

x->+<»

Wyłączamy x przed nawias

lim (x + sin x) = lim

X-»+oo    X—X+°o

Z ostatniego przykładu wiemy, że wyrażenie ", przy x -> +oo, dąży do O,

X

zatem wyrażenie w nawiasie okrągłym dąży do 1. Otrzymujemy

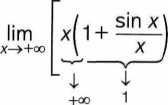
tak więc ostatecznie

lim (x + sin x) = +qo.

X—>+cO

Granice jednostronne funkcji w punkcie

Niech f(x) =    +1i niech (x_n) będzie ciągiem, którego wyrazy x_neS₊(-1)

oraz lim x_n = -1. Wówczas x_n+1 > O i |x„ +1 | = x„+1, zatem

lim f(x_n) - lim

2(x_n+ 1)

V ^xn⁺ 1

+ 1

= 2 + 1 =3.

Jeśli natomiast (x„) będzie ciągiem, którego wyrazy x„eS_(-1) i limx_n = -1, to wtedyx_n +1 <Oi |x_n+1 | = —(x_n+1), zatem

lim f(x_n) = lim

2(x„+1)

-(^Xn+1)

+ 1

= -2+1 = -1.

^/2(x+¹)    ?|

17TTT^{+ 1} '

W tym momencie możemy już stwierdzić, że nie istnieje lim

x->-1

Zauważmy natomiast, że dla dowolnego ciągu (x_n), takiego, że lim x_n = -1, którego

n—ko

wyrazy należą do prawostonnego sąsiedztwa S+(-1) punktu x₀ = -łzawsze

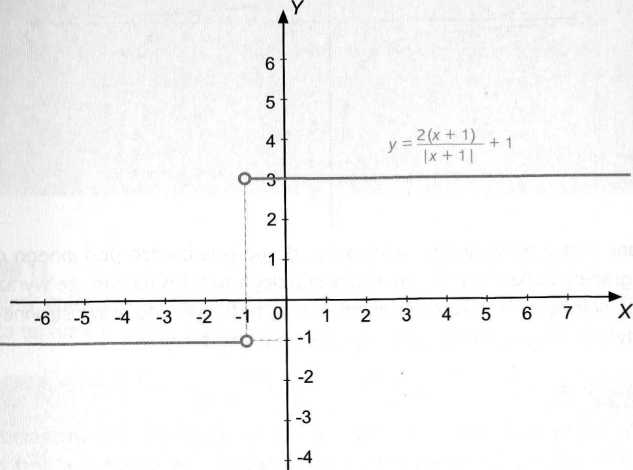
Jim l(x„) - 3. Powiemy w tym wypadku, że funkcja f(x) -    ^{+1 ma}

W punkcie x₀ = -1 granicę prawostronną równą 3.

h idobnie dla dowolnego ciągu (x_n) takiego, że lirn x_n = -1, którego wyrazy nalecą do lewostronnego sąsiedztwa S_(-1) punktu x₀ = -1 zawsze Jim/(x„) = -1.

hiwlemy w tym wypadku, że funkcja f(x) = ^^X+ V+1 ma w punkcie x₀ = -1

granicę lewostronną równą -1.

Jeżeli teraz /(x) = ^ , to biorąc dowolny ciąg (x_n) taki, że Jim^,, ~ O . którego wyrazy należą do prawostronnego sąsiedztwa S₊(0) punktu x₀ = O, mamy |lm/(x_n) = lim — = +oo. Powiemy więc, że funkcja /(x) =^maw punkcie

fl •>'»    n-»oo X_n    X

i

O*

x₀ = O granicę prawostronną niewłaściwą równą +oo. Biorąc teraz dowolny ciąq (x„) taki, że lim x_n = O, którego wyrazy należą do lewostronnego sąsiedztwa

S (O), mamy lim f{x_n) = lim = -qo. Powiemy więc, że funkcja f{x) = - ma

^J n-*cc    n—>oo X_n    ^A

w punkcie x₀ = O granicę lewostronną niewłaściwą równą -<». Oczywiście nie

istnieje lim — .

^J x->0 x