40630 PA274972

ANALIZA STATYSTYCZNA DANYCH

chi_«c<?uiy1 |ZbłółDanycM»I - SPSS Edjyłor

Mit Ectaa Widok Oan© ftzoktttałcarwa Anat

	wejścia	liczebności]
1	A	18.00
'ii-i; *ł	B	22,00;
	' |l	64,00'
.... 4	D	76,00;

Rys. 7.6. Wygląd okna z przykładowymi danymi do jednozmiennowego testu chi-kwadrat Pier* sza zmienna określa kategorie występujące w badaniu, druga jest zmienną pomocniczą i definiuje liczebności poszczególnych kategorii.

Dane dotyczące tego przykładu znajdują się w pliku Rozdział?Jb.sa,v. Teraz tylko ważymy obserwacje przez zmienną „liczebność” (DANE, następnie WAŻENIE OBSERWACJI) i jesteśmy gotowi do rozstrzygnięcia, czy rzeczywiście rację mąjąko* gnilywiści. Aby to uczynić wybieramy ANALIZA, potem TESTY NIEPARAMETBSCZ-NE i na końcu CHI-KWADRAT. Przerzucamy zmienną wejścia (ważne, aby nie po-mylić zmiennych), zaznaczamy opcję do testowania „wszystkie kategorie są równe* (bo taka jest nasza hipoteza zerowa) i klikamy OK Cóż pokazuje SPSS?

wejścia

	Obseiwo waneN	Oczekiwane N	Reszty
A	18	45,0	-27,0
B	22	45.0	-23,0
C	64	45,0	19,0
O	76	45,0	31,0
Ogółem	180

Statystyki testu

	wejścia
CW-kwadrat*	57,333
df	3
istotność asymptotyczna	,000

a 0 komórek (,0<fc) ma liczebność oczekiwaną mniejszą od 5. Minimalna liczebność oczekiwana w komórce wynosi 45,0.

Rys. 7.7. Wydruk raportu SPSS z przykładowymi wynikami badania.

Okazało się, że test „rzutu oka” był trafny. Rzeczywiście mniej szczurów niż oczekiwano wybrało wejścia A i B (w tych. przypadkach uzyskaliśmy ujemne reszty), natomiast więcej zwierząt niż by to wynikało z losowego rozkładu częstości poszło do sera drogą na skróty (dodatnie reszty). Otrzymane zależności obrazuje ryt-

.WNIOSKOWANIE STATYSTYCZNE NA DANYCH JAKOŚCIOWYCH...

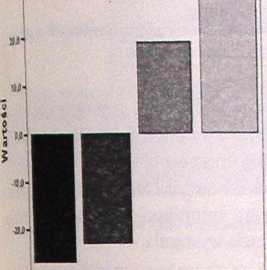
7 8, na którym pokazano wielkości reszt dla poszczególnych kategorii zmiennej trejścia". Aby wykonać taki wykres, należy dwukrotnie kliknąć na tabelę, w któ-jdj znajdują się reszty i następnie wybrać opcję tworzenia wykresu z tabeli.

wejścia

Statystyki Reszty

«>■

i .......-»-1-r

A    I    C    O

wejścia

Rys. 7.8. Wielkości reszt dla poszczególnych kategorii zmiennej .wejścia”. Widać że zdecydowanie rzadziej niż wynikałoby to z losowego rozkładu szczury wybierały wejście A i B, podczas gdy wejścia C i D były wybierane częściej niż losowo.

Okazało się także, że otrzymana wartość statystyki chi-kwadrat jest istotna statystycznie: Chi² (3, N - 180) = 57,33; p < 0,001. Zapis Chi² jest alternatywnym zapisem dla

Test chi kwadrat dla dwóch zmiennych

Chi-kwadrat dla tabel krzyżowych

Wyobraźmy sobie teraz eksperyment, w którym osobami badanymi są klienci kamami. Zawsze, kiedy zamówią kawę kelnerka/eksperymentatorka proponuje im szarlotkę. W połowie przypadków wahającemu się klientowi kelnerka podaje menu ze zdjęciem proponowanej szarlotki, a następnie odnotowuje, czy klient uległ pokusie złożenia dodatkowego zamówienia. W przedstawionym badaniu uzyskano w ten sposób dwie zmienne: zdjęcie (1 - pokazano lub 2 - nie) oraz zamówienie na szarlotkę (1 - złożone bądź 2 - nie). Prawidłowe wprowadzenie danych do pakietu SPSS wymaga zdefiniowania takich właśnie dwóch zmiennych oraz opisanie za ich pomocą każdej z osób badanych (plik z danymi Rozdzial7_c.sav).