57559 PA274992

ANALIZA STATYSTYCZNA DANYCH

Krok pierwszy - wprowadzenie danych DO EDYTORA DANYCH SPSS

Dane, na których można wykonać analizę wariancji, wyglądają podobnie jak te, na których przeprowadzamy test t-Studenta dla prób niezależnych. Plik z danymi (Rozdzial9_a.sav) zawiera dwie zmienne, pierwsza z nich określa przynależność do grup, druga poziom zmiennej zależnej. Tak więc, gdy zerkniemy do danych zobaczymy, że kolumna pierwsza (SKUT) zawiera wartości zmiennej zależnej, natomiast kolumna druga (WLAD) zawiera wartości od 1 do 3, oznaczające warunek badawczy. Wprowadzając dane, pamiętajmy o opisie wartości zmiennej niezależnej - ułatwi to potem interpretację wykresów oraz zrozumienie wydruku.

Krok drugi - sprawdzenie założeń nałożonych na dane

Gdy zbiór danych jest gotowy, przystępujemy do sprawdzenia, czy dane spełniają założenie o normalności rozkładów' wyników w grupach. Ponieważ testując różnice opieramy' się na średnich, a te są statystykami bardzo czułymi na wyniki nietypowe, warto sprawdzić, czy nie występują one w danych. Te wstępne analizy - statystyki opisowe i wykresy skrzynkowe - najszybciej wykonamy wykorzystując opcję EKSPLORACJA w menu ANALIZA -4 OPIS STATYSTYCZNY (patrz: rys. 9.1).

Rys. 9.1. Okno główne funkcji EKSPLORUJ DANE.

W oknie głównym EKSPLORACJA definiujemy zmienną zależną przenosząc jej nazwę z lewego okna za pomocą strzałki do okienka ZMIENNE ZALEŻNE oraz zmienną niezależną w analogiczny sposób przenosząc ją do okienka LISTA CZYNNIKÓW (patrz: rys. 9.1).

Funkcja ta pozwala sprawdzić normalność rozkładów wyników w grupach, wyśledzić wyniki nietypowe oraz sprawdzić, czy wariancje w porównywanych grapach są do siebie podobne, co jest istotne dla wiarygodności wyników uzyskanych w jednoczynnikowej analizie wariancji.

9 • JEDNOCZYNNIKOWA ANALIZA WARIANCJI..,

Rys. 9.2. Okno WYKRESY w funkcji EKSPLORACJA DANYCH.

W menu WYKRESY w oknie EKSPLORACJI do opcji zaznaczonych standardowo wybieramy dodatkowo WYKRESY NORMALNOŚCI Z TESTAMI oraz w części ROZRZUT-POZIOM Z TESTEM LEVENE’A opcję NIE PRZEKSZTAŁCONE (rys. 9.2).

Jeśli mamy przypadki nietypowe (outliers), najłatwiej wyśledzimy je za pomocą wykresów skrzynkowych, których wykonanie zleciliśmy w EKSPLORACJA, zaznaczając WYKRESY SKRZYNKOWE.

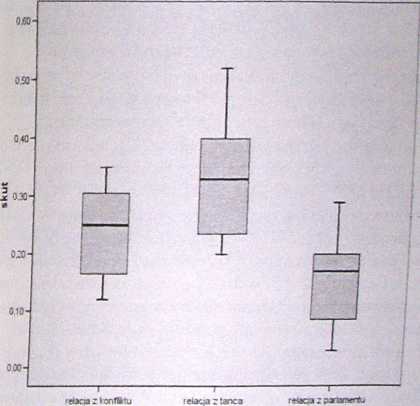
wiad

Rys. 9.3. WYKRESY SKRZYNKOWE pokazujące własności rozkładu wyników w poszczególnych grupach.

Wykres}' skrzynkowe (patrz: rys. 9.3) wskazują, że w żadnej z grup nie ma wyników nietypowych (szczegóły w Rozdziale 3).

215