62093 Strona 1 (12)

STATYSTYKA MATEMATYCZNA

Estymacja przedziałowa parametrów

• Przedział ufności dla średniej

Model I

Badnnn cecho u populacji generalnej ma rozkład normalny N (u. er). Wartość średniej // jest nieznana odchylenie standardowe er w populacji jest znane /. populacji tej pobrano próbę o liczebności /»elementów, wylosowanych niezależnie Przedział ufności dla średniej u populacji otrzymuje się ze wzoru

_r, I O a '

r ■ ,v u < u < x + u_u ■•=■-, = I - a

:n " \ >i j

gdzie

//„

- test pniwtlopodobienstwem. przejętym z góry i nazywanym Hs/>iih'\iiitikic^,iii ufiwści tw zastosowaniaeb praktsczmcli przy imuje się wartość /-« >0,9)

- test wartością zmiennei losowej t o rozkladz.ie normalny m standaryzowany m

- średnia arytmetyczna z próby obliczona wg zależności

M-c

U artość «„ dla danego wspolczs unika ufności i-a wy znacza się z rozkładu normalnego standaryzowanego N(0. I). w taki sposób, by spelmon;i była relacja

Pj-ti., ■ y •- u, I I-o,

/ „jest taka wartoseta zmiennei losowei o rozkładzie normalnym standaryzowanym, ze pole powierzchni pod krzy wa gęstości w przedziale (-u.,. u . j wmiosi I-i/, a pole pod krzy wa gęstości na prawo od u, i na lewo od -u. wynosi po u 2 1 ,.|cst można równie/, wyznaczyć na podstawie dy slrybuanly z zależności:

c!>(// t - I - (u !2)

(gdzie <bt») icst dyslrybuanta rozkładu normalnego standaryzowanego), korzystając z tablic rozkładu normalnego / „jest nazywane kwaim leni rozkładu normalnego

Model II

Badana cecha w populacji generalnej ma rozkład normalny 'stu. o) Nieznana jest zarówno wartość średnia u. tak i odchylenie standardowe rrw populacji

/ populacji tej wylosowano niezależnie mała próbę o liczebności n (n '0) elementów Przedzuil

ufności dla średniej u populacji otrzymuje się wówczas z wzoru

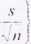
- a

gdzie

n - I

jest odchyleniem standardowym z próby

W‘ailość / o/nacza wartość zmiennej / Studenta odcz\lan;| / tablice tego rozkładu dla //-/ stopni swobody u taki sposób. b\ dla danego / gói> prawdopodobieństwa l-u. spełniona byki relacja

1’i-l.. t t. ! I-k

Sposoby wyznaczaniii wartości s.( podobne jak w modelu I

Model III

Badana cecha w populacji generalnej ma rozkład normalns Nip. et) bądź dowolny inny rozkład o średniej fi i skończonej wariancji rr (nieznanej) /. populacji tej pobrano do próby » niezależnych obserwacji, przy czym liczebność próby jest duża (co najmniej kilkadziesiąt). W tedy przedział ufności dla średniej u populacji wyznacza się ze wzoru pik w modelu I. z ta tylko różnica. ze zamiast rrwe wzorze tym u/ywatm wartości odchy lenia standardowego \ z próby

Zada nic 1

Wytrzymałość materiału budowlanego jest zmienna losową o rozkładzie normalm m N(u. a). W celu oszacowania nieznanej średniej u wy trzymałości tego materiału dokonano pomiaru wytrzymałości na n-5 wylosowanych niezależnie elementach z. lego materiału Otrzymano następujące wy niki: 20 4. 10.6. 22.1. 20 8. 21 I

Przyjmując współczynnik ufności l-(/.-0.00 zbudować przedział ufności dla średniej wytrzymałości u tego materiału.

Zadanie 2

Chcemy oszacować średni staż pracy pracowników zatrudnionych przy obsłudze komputerów w Gliwicach. W tym celu. stosując losowanie nieograniczone, niezależne, wylosowano z populacji tych pracowników próbę liczącą n= 100 osób i otrzymano następujące wyniki badania stażu pracy:

0-2	4
2-4	!()
4-6	5 5
6-8	25
8-10	6

Przyjmując współczy nnik ufności l-a=0.90 zbudować przedział ufności dla średniego stażu pracy badanej populacji pracowników

Zadanie 3

Oszacować żywotność (w godzinach świecenia) wyprodukowanej partii świetlówek W iadomo, że czas świecenia świetlówek ma rozkład normalny z odchyleniem standardowym 0=120 godzin Wylosowana niezależnie / lej partii próba n=25 świetlówek, dala następujące w yniki pomiarów czasu ich świecenia w godzinach 2630. 2820. 2900. 2810. 2770.

2840. 2700. 2950. 2680. 2720.

2800. 2970. 2680. 2660. 2820.

2580. 2840. 3020. 2780. 2920.

3060. 2840. 2550. 2790. 2850

Przyjmując współczy nnik ufności 0.98 oszacować metodą przedziałową średni czas świecenia świetlówek tej partii.