61161 stat Page7 resize

37

Statystyki! matematyczna

3.5.1 Przedział ufności dla średniej w modelu normalnym ze znaną wariancją

Niech Xi, X2,..., X_n będzie próbą z rozkładu normalnego iV(/i,<7²), przy czym wartość <7² jest już nam znana. Jedynym parametrem modelu jest więc zatem fx. Ponieważ

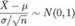
(3.66)

z tzw. twierdzenia o standaryzacji, więc

gdzie z j_£s jest kwantylem ze standardowego rozkładu normalnego o rzędzie /?. Mamy zatem wzór na przedział ufności w postaci

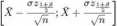
(3.67)

(3.68)

3.5.2 Przedział ufności dla średniej w przypadku nieznanego odchylenia standardowego

Załóżmy, że próba Xi, X2,..., X_n pochodzi z rozkładu normalnego N(fx, <7²), przy czym tym razem również wariancja jest nieznana. Możemy stworzyć wtedy odpowiedni przedział ufności dla średniej i w takim przypadku. Zachodzi

(3.69)

gdzie t(n — 1) oznacza rozkład t-Studenta z n - 1 stopniami swobody. Stąd

(3.70)

gdzie t\Ą£ _nl jest kwantylem rzędu dla rozkładu t-Studenta on-1 stopniach swobody. Prowadzi to do przedziału ufności postaci

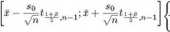
(3.71)

Uwaga! Należy podkreślić różnicę pomiędzy przedziałami ufności (3.68) i

(3.71). Pierwszy z nich można zastosować tylko wtedy, jeśli informacja o odchyleniu standardowym (lub wariancji) jest już nam wcześniej znana. Gdy natomiast odchylenie standardowe (lub wariancję) liczymy na podstawie tej samej próbki, co i średnią, wykorzystać musimy przedział (3.71).

3.5.3 Przedział ufności dla wariancji

Podobnie jak poprzednio, niech Xi,X2,...,X_n ~ N((x,<r²). Możemy stworzyć przedział ufności dla wariancji. Ponieważ

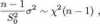
(3.72)