63960 skan0295

298 Elektrochemia

a stąd

(6)

_ (^soli ⁽-H⁺) ^aAc~~ ę ®    )^;± •>

gdyż dla elektrolitu 1-1, zgodnie z teorią Debye’a-Hiickla, y_± = y_ = y+. Współczynnik aktywności niezdysocjowanego kwasu jest równy 1, a zatem

(7)

_ (<T ~ ^CH⁺) ^flHAc ~ _c®

c_H+ (oznaczone, jak poprzednio, przez x) oraz y_± wyznaczymy z wyrażenia na 7C_a:

„ _ (aH^+aAc-) _ x{c_soh + x)yl

-‘'-a    /    \ @    ‘

«HAc    (c_k-*)c®

Po jego przekształceniu dostajemy równanie kwadratowe

x²yl + x(c_souy± + A'_ac®) -K._dc_kc® = 0.    (8)

Tak jak poprzednio, metodą kolejnych przybliżeń, znajdujemy stężenie jonów H⁺ i współczynnik aktywności, który obliczamy, korzystając z prawa De-bye’a-Huckla (6.39):

0,509111 • (-1)lV(^cs„ii + *) lgy± =--i -•

1 + Wsoli + ^X)

Wyniki obliczeń zestawiono w tab. 6.12.

Tabela 6.12

i	7[M]	log y±	y±	A		^xi [M]		aH-		pH
1			1	1,001 •	10“^2	1,753	10“^5	1,753 •	10“^5	4,756
2	0,1000	-0,12232	0,755	3,247	10“^3	3,079	lO"^5	2,323 •	io~^5	4,634
3	0,1000	-0,12233	0,755	3,247	10~^3	3,079	io--^5	2,323 •	10"^5	4,634

W tym przypadku już dla i = 3 otrzymujemy poprawmą wartość x oraz y_±. a pH obliczamy korzystając wprost z definicji:

pH = -lg a_H+ = -lg

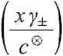
-Ig

3,079-10-⁵-0,755

1

4,634.

W obliczeniach przybliżonych korzysta się ze wzorów (5)—(7), przy czym pomija się stężenie jonów H⁺ jako bardzo małe w porównaniu ze stężeniem soli czy kwasu, a także przyjmuje się, że y± = 1. Wówczas wyrażenie (5) przybiera spotykaną często postać