66962 skanuj0071 (15)

138 5. Równowagi jonowe w rozcieńczonych rortworath wpfrffŁ

UPROSZCZONY MODEL MATEMATYCZNY II . Uproszczenie modelu 2

* Zakładając, że w bilansie materiałowym (4.5) stężenie jest małe w porównaniu z ci można je pominąć, otrzymuje się:

«'^CHNO,    ⁽⁴'²¹⁵|

Uproszczony model matematyczny II stanowią równania (4.3), (4.4), (4.7), (4,10) | oraz (4.21). Pamiętając, że również w tym przypadku słuszna jest zależność

Obliczenia Podstawiając dane liczbowe otrzymuje się;
dla c = 0,5 mol/dm^3 -	a-0,035;
dla c-0,1 mol/dm^5 -	a =*0,079;
dla c » 0,01-mol/dm- —-diacf 0,001 mol/dm^3 -	rtsaft.OSI*-	* ___
	a-0,794.		-49

Weryfikacja uproszczenia

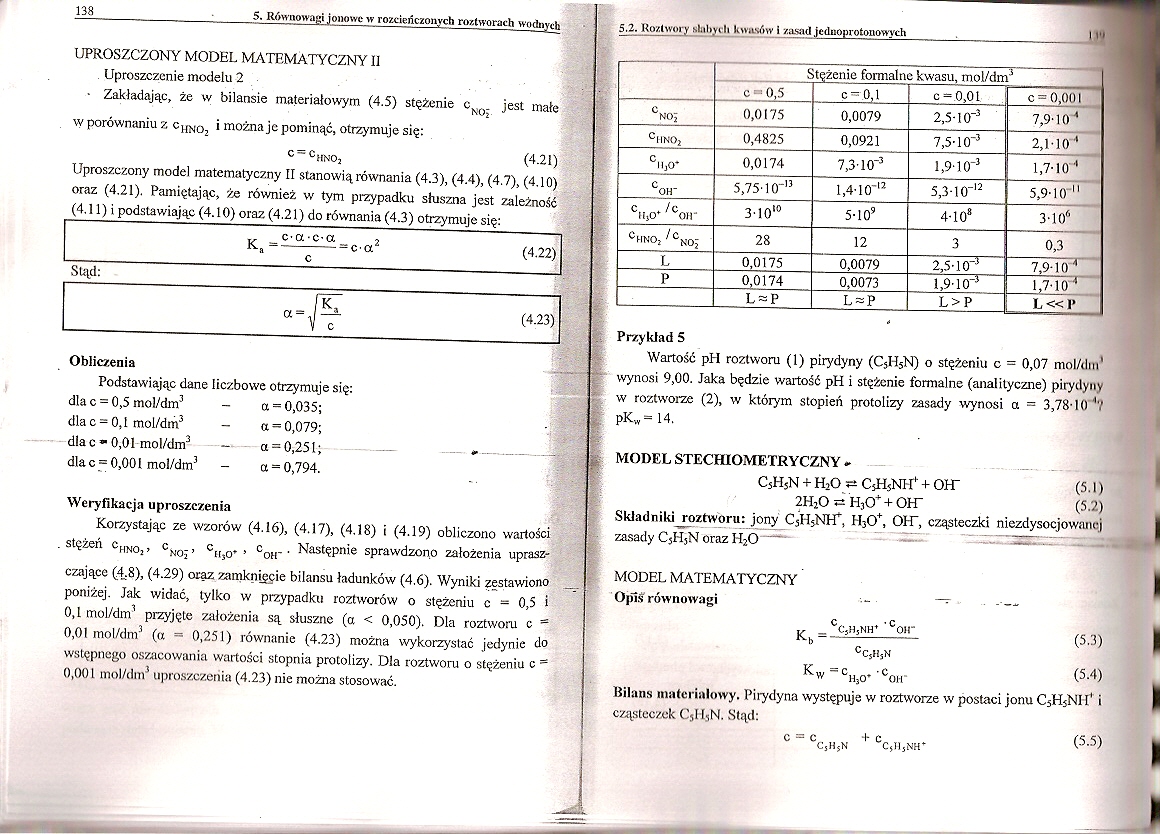
Korzystając ze wzorów (4.16), (4.17), (4.18) i (4.19) obliczono wartości stężeń c_HNOjł c^., c_||jQ., c^.. Następnie sprawdzono założenia uprasz- ‘¹

czające (^.8), (4.29) orąz zamknięęie bilansu ładunków (4.6). Wyniki zestawiono¹' ? poniżej. Jak widać, tylko w przypadku roztworów o stężeniu c = 0,5 i 0,1 mol/dm³ przyjęte założenia są słuszne (a < 0,050). Dla roztworu c -0,01 mol/dm³ (a = 0,251) równanie (4.23) można wykorzystać jedynie do wstępnego oszacowania wartości stopnia protolizy. Dla roztworu o stężeniu c * 0,001 mol/dm³ uproszczenia (4.23) nie można stosować.

	Stężenie formalne kwasu, mol/dm^3
	c-O.S	0*0,1	c-0.01	c = 0.001 L
fi NOJ	0,0175	0,0079	2,5-10"^3	7,9-10“*
^cIINOi	0,4825	0,0921	7,5-10"^5	2,1-10"*
c IIjO	0,0174	7,3-lO^	1,9*10*	1,7-10“*
^COH*	5,75- ur^n	1.4-10"'^2	53i<r^12	5,9-10"^11
^Cii^* ^/co*r	310*	5-lC^	4-10*
°'"'^,01^/CKOi	28	12	3	05 1
L	0.0175	0.0079	W-KT*	7.9-10^4
P	0.0174	0.0073	14-10-*	1.7-ir*
	L = P	L=P	L>P	L«P

(5.3)

(5.4)

CsHjNH* i

(55)

1

_ ^CC₅H_łMH* ‘ ^co»r --

^CC»M|H

^KW “^C„_ł0. ^COH-

Bilans materiałowy. Pirydyna występuje w roztworze w postaci jonu cząsteczek CjH₅N. Stąd:

c ** c + C_

C,H,H C,II,W