73648 SNC03662

GC + C = O + 2eov sin q>=O

p A*

1 Ap * 2pcosin cp Ax

Przy tym samym gradiencie ciśnienia prędkość wiatru geostroficznego jest większa, gdy sin ę, czyli szerokość geograficzna jest mniejsza. Na półkuli południowej prędkość wiatru geostroficznego oblicza się z analogicznego wzoru, więc jej wartość będzie identyczna, natomiast kierunek będzie przeciwny, ponieważ siła Coriolisa działa tam na lewo od kierunku prędkości.

7.3. Wiatr gradientowy

W rzeczywistej atmosferze izobaty rzadko przyjmują idealnie prostoliniowy kierunek, a to oznacza, że oprócz sil gradientu ciśnienia i Coriolisa działa także siła odśrodkowa. Jej wartość zależy od promienia krzywizny izobar r oraz od prędkości wiatru | Rozważmy wyidealizowany przypadek, w którym izobaty są kołowe (rys. 7.10). Wiatr, jaki wieje w swobodnej atmosferze, czyli powyżej warstwy tarcia, wokół kołowych izobar nazywamy wiatrem gradientowym.

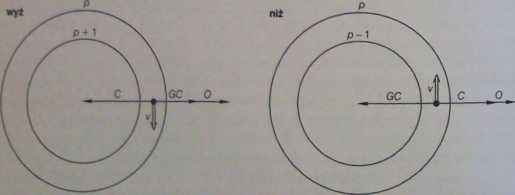
tyi. 7. ł O. Wiatr gradientowy w niżu i wyżu na półkoli północnej; CC - sita gradientu ciśnienia, C-siła Coriolisa, O - sita odśrodkowa, v—wiatr

W niżu siła gradientu ciśnienia skierowana jest do jego środka, a siła odśrodkowa Corioiaa na zewnątrz. W wyżu siła gradientu ciśnienia skierowana jest na zewnątrz, odobnie jak siła odśrodkowa. Ich suma jest równoważona przez siłę Coriolisa. W wa-inkach równowagi prędkość wiatru v_r musi spełniać równanie

GC + C ±0 = 0

lak + odpowiada wiatrowi gradientowemu w niżu, znak - w wyżu.

1 Ap „    łjr _n

- -•    + 2iov_ sin — = O

p AZ ^r    r

Po rozwiązaniu równania kwadratowego względem v_p otrzymujemy dla wiatru gradientowego w niżu

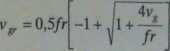
a dla krążenia powietrza w wyżu

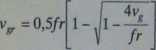
gdzie: /- parametr Coriolisa (f = 2a>sinq>), v_g - prędkość wiatru geostroficznego, jaki wiałby na tej samej szerokości geograficznej przy tym samym gradiencie ciśnienia.

Wiatr gradientowy, podobnie do geostroficznego, wieje równolegle do izobar, pozostawiając niższe ciśnienie na półkuli północnej po lewej stronie, a na półkuli południowej po prawej stronie. Oznacza to, że na półkuli północnej powietrze krąży wokół niżu w kierunku przeciwnym do ruchu wskazówek zegara, a wokół wyżu w kierunku zgodnym ze wskazówkami zegara. Jednocześnie, przy tym samym gradiencie ciśnienia, wokół niżu wiatr krąży z szybkością mniejszą od prędkości wiatru geostroficznego i z tego powodu nazywany jest wiatrem subgeostroficznym. Wokół wyżu prędkość wiatru gradientowego jest większa od prędkości wiatru geostroficznego i dlatego nazywany jest wiatrem supergeostroficznym. Wyrażenie

Ro =

nosi nazwę liczby Rossby'ego. Z równań prędkości wiatru geostroficznego widać, że w przypadku wyżu rozwiązania rzeczywiste istnieją tylko wówczas, gdy liczba Ross-by ego Ro 5 1/4. W przeciwnym razie wartość wyrażenia pod pierwiastkiem byłaby ujemna. Oznacza to, że w wyżu krzywizna izobar i gradient ciśnienia nie mogą przekroczyć pewnego progu, ciśnienie musi spadać łagodnie od środka na zewnątrz układu, a izobary nie mogą zbyt gwałtownie zakręcać. Takie ograniczenia nie występują w przypadku ośrodków niskiego ciśnienia. Ta ważna prawidłowość znajduje odzwierciedlenie w rzeczywistym rozkładzie ciśnienia i cyrkulacji atmosferycznej na Ziemi. Największe poziome gradienty ciśnienia i krzywizny linii prądów powietrznych występują z reguły w układach niżowych.

Wiatr geostroficzny i gradientowy są skierowane równolegle do izobar. Jeżeli z wysokością zmienia się kierunek lub gęstość izobar, zmieni się również prędkość i kierunek wiatru. Jedyną przyczyną zmian kierunku lub gęstości izobar w atmosferze są różnice temperatury. Oznacza to, że wraz ze wzrostem wysokości wiatr geostroficzny uzyskuje dodatkową składową prędkości zależną od kierunku i wartości gradientu temperatury. Ta dodatkowa składowa skierowana jest wzdłuż średniej izotermy w warstwie między dwiema powierzchniami i chłodniejsze powietrze leży po jej lewej stronie. Ponieważ nierównomierny rozkład temperatury jest główną przyczyną zmian wiatru geostroficznego, ta dodatkowa skiadaft^nsi nazwę wiatru termicznego.