73847 Str106

20# A Kr*v« i eliptyczne

Definicja. Niech K będzie krzywą eliptyczną nad ciałem liczb rzeczywistych t niech P i Q będą dwoma punktami tej krzywej. Definiujemy punkt przeciwny do P i sumę P i- Q w następujący sposób:

J. Jeśli P jest punktem w nieskończoności O, to definiujemy -P - O oraz P -i Q = Q; zatem punkt O jest elementem neutralnym (czyli zerem) grupy punktów. W dalszym ciągu zakładamy, że ani P, ani Q nic jest punktem w nieskończoności.

2.    Element przeciwny - P jest to punkt o tej samej współrzędnej a, co punkt P, ale przeciwnej współrzędnej y, tzn. — (jc, y) = (a*, —;>). Z równania (1) wynika oczywiście, żc jeśli punkt (a, r) leży na krzywej, to punkt (a, -y) też leży na tej krzywej.

3.    Jeśli punkty P i Q mają różne współrzędne x, to nietrudno zauważyć, żc prosta / = przecina krzywą w jeszcze dokładnie jednym punkcie R (chyba żc ta prosta jest styczna do krzywej w punkcie P i wtedy bierzemy R = P lub jest styczna w punkcie Q i wtedy bierzemy R = Q). Teraz jako P + Q bierzemy punkt —R, tzn. punkt symetryczny (względem osi x) do tego trzeciego punktu przecięcia. Konstrukcja geometryczna punktu P + Q jest pokazana w przykładzie 1, poniżej.

4.    Jeśli Q = — P (tzn. punkt Q ma tę samą współrzędną a, ale przeciwną współrzędną y), to definiujemy P + Q = O (punkt w nieskończoności). (Jest to wymuszone przez warunek (2).)

5.    Ostatnią możliwością jest P = Q. Niech prosta / będzie prostą styczną do krzywej w punkcie P i niech R będzie jedynym punktem przecięcia prostej / z krzywą, różnym od P. Wtedy definiujemy P + Q = —R. (Jeśli prosta / jest „podwójnie styczna” do krzywej, tzn. gdy P jest punktem przegięcia krzywej, to jako R bierzemy sam punkt P.)

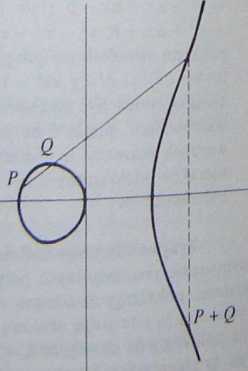
Przykład 1. Krzywa eliptyczna o równaniu y² = a³ — a na płaszczyźnie jest przedstawiona na rysunku po prawej stronie. Widać na nim również typowy przypadek dodawania dwóch punktów P i Q. Rysujemy cięciwę przechodzącą przez punkty P i Q i jako P + Q bierzemy punkt symetryczny (względem osi a) do trzeciego punktu przecięcia prostej przechodzącej przez P i Q z krzywą.

Jeśli punkty P i Q pokrywają się, tzn. gdy chcemy znaleźć punkt 2P, rysujemy prostą styczną do krzywej w punkcie P; wtedy punktem 2P jest punkt symetryczny do trzeciego punktu, w którym ta styczna przecina krzywą.

Pokażemy teraz, dlaczego istnieje dokładnie jeden punkt, w którym -rosta /, przechodząca przez punkty P i g, przecina krzywą; jednocześnie wyprowadzimy wzory na współrzędne tego trzeciego punktu, a zatem i wzory na współrzędne sumy P + g.

Niech (xj, y_{), (x₂, yi) • fe, ?j) oznaczają odpowiednio współrzędne punktów P, g i P + Q. Chcemy wyrazić x₃ i y₃ za pomocą współrzędnych x,_t y_v x_z i jy Przypuśćmy, że mamy do czynienia z przypadkiem (3) definicji sumy P + g i niech y = cłx + p będzie równaniem prostej przechodzącej przez punkty P i 6 (w przypadku (3) ta prosta nie jest pionowa). Wtedy a = (y₂ - y\)l(^x2 - ^xi) oraz f = y_{-ix_v Punkt prostej /, tzn. punkt (x, ax + P) leży na krzywej eliptycznej wtedy i tylko wtedy, gdy iix + p)² = * x³ + ax + b. Zatem dla każdego pierwiastka równania trzeciego stopnia x³ - (ax + /O² + o* + b = 0 istnieje jeden punkt przecięcia. Znamy jednak dwa pierwiastki tego równania: x, i x₂, gdyż (x_A, ax, + p) i (x₂, zx₂ + fi) są współrzędnymi punków P i g leżących na tej krzywej. Ponieważ suma pierwiastków unormowanego równania trzeciego stopnia jest liczbą przeciwną do współczynnika przy x², więc trzecim pierwiastkiem tego równania jest x₃ = ol² — x_A - x₂. Prowadzi to do następujących wzorów na x₃ oraz P + g = (x₃, -(ax₃ + p)) wyrażonych w zależności od x_v y_tJ x₂ i >*₂:

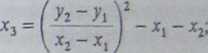
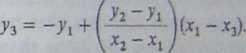
Przypadek (5), gdy P = g, jest podobny, z tym tylko, że współczynnik a jest teraz równy pochodnej dyjdx w punkcie P. Różniczkowanie funkcji uwikłanej w równaniu (1) prowadzi do wzoru a = (3x² + a)l2y_v z którego otrzymujemy następujące wzory na współrzędne punktu 2P:

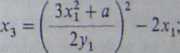
(5)

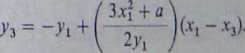
Przykład 2. Niech P = (-3, 9) i g = (-2, 8) będą punktami krzywej o równaniu y² = x³ — 36x. Wyznaczmy punkty P + g i 2P.

Rozwiązanie. Podstawiając x_A = -3, y_{ = 9, x₂ = -2, y₂ - 8 do pierwszego ze wzorów (4), otrzymujemy x₃ =?■ 6; wtedy drugi z tych wzorów daje y₃ — 0. Następnie, podstawiając x_A = - 3 i y_x = 9 do pierwszego ze wzorów (5), otrzy-