78460 new 98

200

7. Zasady obliczeń wytrzymałościowych śrub

Przykład 7.5. Zaprojektować podnośnik śrubowy o nośności Q = 7200 N napędzany przez śrubę pokrętłem korbowym. Wysokość złożonego podnośnika H = 540 mm.

Przed rozpoczęciem obliczeń sporządzamy rysunek wstępny podnośnika (rys. 7.58). W podnośniku zamiana ruchu obrotowego korby na ruch posuwisty nakrętki realizowana będzie za pomocą przekładni zębatej z kołami stożkowymi. Śruba nośna podnośnika jest tu rozciągana a korpus ściskany. Długość wyboczeniowa korpusu l — 360 mm.

Obliczenie śruby

Średnice rdzenia gwintu obliczymy z warunku wytrzymałości złożonej według wzoru (7.28)

> *'²⁷ i/x ■=⁹'¹ mm'

R 280

gdzie k_r =    — —-— = 140 MPa jest dopuszczalnym naprężeniem przy

rozciąganiu, R_e — 280 MPa — granicą plastyczności stali St5 przyjętej według PN-72/H-84020 na śrubę, X_e = 2 — współczynnikiem bezpieczeństwa.

Warunkowi temu odpowiada gwint Trl2X2, dla którego d₃ = 9,5 mm, d₂ = D₂ = d_t= U mm, D₄ = 12,5 mm, D_x = 10 mą a_r = y = 15°,

P    o

y = ^ardtg    ^{= 3X0} tg—rr = 3°19'.

Przyjęte wymiary gwintu należy sprawdzić według wzoru (7.22) oz = ) V+3z² = /l01,6²+3-50,6² == 134,2 < k_r = 140 MPa,

gdzie:

Q    7200

° “    --~ = 101,6 MPa

4    4

jest naprężeniem rozciągającym,

x

M_s

W„

M_s

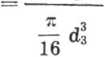
16^8515

= 50,6 MPa

— naprężeniem skręcającym,

M, —0,5Qd_t'tg(y+e') — 0,5-7200-ll-tg(3o₁₉'₊₈o₅o') ₌ 3525 N-mm, — momentem skręcającym śrubę,

7.7. Przykłady obliczeniowe

201

q — aro tg

cos a_r

= arc tg

0,15

cos 15

8°50'

— pozornym kątem tarcia, a /i = 0,15 — założonym współczynnikiem tarcia.

Przyjęte wymiary gwintu spełniają warunek wytrzymałości.

i

Obliczenie korpusu

W przypadku złożonego kształtu przekroju wygodniej jest wstępnie założyć jego wymiary, a następnie sprawdzać współczynnik bezpieczeństwa. Zakładamy więc, że korpus o przekroju jak na rys. 7.59 wykonany

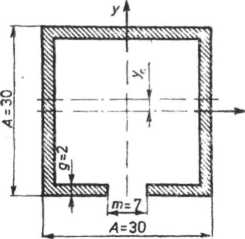
Rys. 7.59. Przekrój poprzeczny korpusu podnośnika

zostanie ze stali St3, dla której (tablica 7.3) R„ = 310 MPa, Ri = 1,19 MPa. Pole przekroju wynosi F = 2(A — 2g)g+Ag+(A—m)g = 2(30—4) + 30-2 + + (30—7)-2 = 210 mm. Środek ciężkości przekroju jest przesunięty względem środka kwadratu AXA o wielkość

mg-

yc =

7-2-14

F    210

stąd minimalny moment bezwładności przekroju

Imtn - 2

12

+ gAy_c

H

= 0,93 mm,

^W-²⁹+ ₊ W-2<,)p(-A+L

A — m — 2g ,

i:

g* + (A-m-2g)g

12

A-g ,

4\

yc

9 • tn³

= 2—i^ —+ 2-30-0,93²-

+

26- 2^!

12

+ 26-2-13,072+

19-2³

12

+ 19-2 -14,93² = 21935 mm².

Z rysunku wstępnego mamy wysokość korpusu I = 360 mm. Dla I przypadku wyboczenia swobodna długość wyboczeniowa l, = 21 = = 720 mm. Smukłość korpusu wynosi