88763 P3200180

czy tez statystyki Gowera

(4.114)

(4.115)

G= Z(d_n-c_a)²

i jej odmiany w postaci ważonej sumy kwadratów¹⁰¹ WSK = 2 w_n(d_n - cj²

które są miarami niezgodności (lub dopasowania) między macierzą odległości D a poziomami łączenia na dendrogramie.

Powyższe wskaźniki można uogólnić w formie metryki Minkowskiego

dla 0 < m < 1

(4.116)

oraz

max| d_n — c_n |    dla m = 0

(4.117)

lardine i Sibson w roku 1968 zaproponowali serię względnych miar opartych ma metryce Minkowskiego. które można zapisać w następującej ogólnej postaci

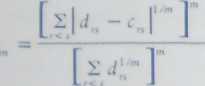
ó

(4.118)

gdzie 0< m < l. Miary dopasowania według powyższej propozycji są niczym innym jak standaryzowanymi metrykami Minkowskiego, w których poprzez różniące się wartości m można różnicować wagi dużych lub małych różnic zarówno odległości, jak i wartości kofenetycznych (zob. Sneath i Sokal, 1973; Everitt, 1978). Wartości miar i =0 wskazują na dopasowanie doskonałe. Jardine i Sibson, objaśniając istotę miary, stosowali m = 1 / Z a więc analogicznie jak w przypadku znanego z zastosowań w niemetrycznym skalowaniu wielowymiarowym, a wprowadzonej w 1964 roku przez Kruskala mierze o nazwie STRESS (ang. standarized residual sum of square)

1/2

(4.119)

.

gdzie c_n są elementami macierzy kofenetycznej.

Wartości miary stress dla poszczególnych metod grupowania podano w ostatnim wierszu tablicy 4.6.

Zauważmy, że współczynnik korelacji kofenetycznej i miary dopasowania <5 czy d_m nie muszą dawać takiej samej oceny grupowania. Jeżeli bowiem założymy, ze jakaś metoda grupowania hierarchicznego rozszerzyłaby proporcjonalnie ^i0! Pomysł na porównanie macierzy odległości (lub podobieństwa) przy użyciu tej miary jest przy pisywany J A. Hartiganowi (1967 r.j; zob. Anderberg (1973).

— 1). natomiast wskaźnik ó przyjąłby wartość równą A — £4, i świadczyłby o wyjątkowo dużej niezgodności. Idlatego wskaźniki ó czy ó_m nic są allernaty wą

dla współczynnika korelacji kofenetycznej Mają one inną wariośt informacyjną

oceniają inne własności grupowania

Czasami można zakładać, że w obserwowanych odległościach lub pod o bieństwach znaczenie ma tylko porządek, a nie bezwzględne poziomy łączenia Wówczas miarą ogólnego dopasowania dendrograinu może byc współczynnik

korelacji rang lub na przykład współczynnik y Goodmana-Kruskala o postać i

(4 120

(C-D)

^Y~ (C + D)

gdzie C oraz D oznaczają odpowiednio liczby zgodnych (ang. concordant ) i nie zgodnych (ang. discordant) par {(r, s),

Współczynniky porownuje zatem wszystkie pary obiektów ze względu na od ległość (lub podobieństwo) między nimi, czyli wszystkie pary odległości w ma cierzy odległości i macierzy dendrogramu. Porów nanie między parami < r s i( r u można zapisać w postaci relacji d_fi R_dd_tu oraz c_n R c_m gdzie symbole R i R oznaczają relacje mniejszości (<) i w iększości (>). Jako parę zgodną określimy laką parę, dla której (R_d ,R₍) = (<> <) lub (R, , R,)« (>,>)■ Rozbieżność znaków nie równości jest świadectwem niezgodności. Współczynnik y opiera się na ląc / no liczbie zgodnych i niezgodnych par (pomija się w nim wartości remisowe. Po dobnie jak współczynnik korelacji przyjmuje on w artości / przedziału — 1 < y < i od pełnej niezgodności do pełnej zgodności (/<*b. Gordon. 1999 Współczynnik y Goodmana-Kruskala jest także miarą efektywności różnych metod grupowania stosowanych do tych samych danych.

Zapewne mniej znaną i rzadziej stosowaną miarą zgodności dwóch ugrupo wań jest współczynnik Randa. W. Rand zaproponował go w 1971 roku dla oceny

podobieństwa dwóch podziałów’, powiedzmy: P = {C .( _: .....C_k) } oraz

P₂ = {C,₂,C₂₂,C\₂), które spełniają kryteria podane w punkcie 4.2. Współczynnik zdefiniowano następująco

RAND =

*(*-1)

2

(4.121)

pierwszym etapie łączenia zachowana zostaje rzeczywista odległość dwóch najbardziej podobnych obiektów

Współczynnik Goodmana i Kmskala jest zasadniczo stosowany do oceny zgodności upo rządkowań i może być wykorzystywany do grupowania zmiennych (por. współczynnik r-Kcndalla).