Image20

38

ODPOWIEDZI I ROZWIĄZANIA

I. MECHANIKA KLASYCZNA

1. KINEMATYKA

1.1.

a)    r, = 9,4 [m], r₂ = 11,3 [m];

b)    r = —2t + 7/ - 3 U[m], r = 7,9 [m];

c)    cos (r",, r₂) = 0,7, cos (r_l, r) = 0,5, cos (r₂,    = 0,9;

II

1.2.

a. Z definicji prędkości

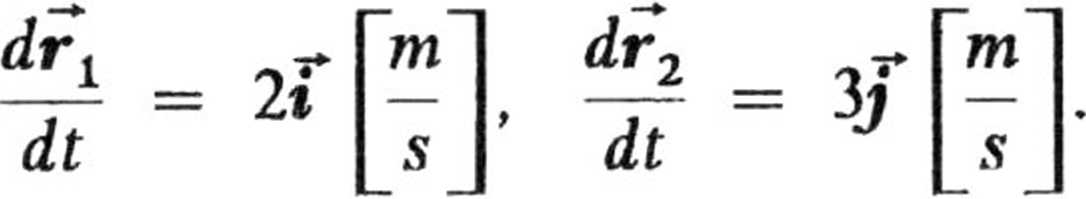
Całkując te wyrażenia i korzystając z warunków początkowych dostajemy

^ = (21 - 3) T [m], r₂ = (31 - 3) / [m],

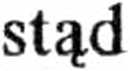
^r = ^r2 - ^rl

(3 - 2t) t + (3t - 3) / [m]

b. Obliczając minimum funkcji r = r(t) znajdujemy czas największego zbliżenia t_min = 1,2 [s] oraz odpowiadającą mu odległość r_min = 0,8 [m].

1.3.)

a) v = v₂ -    = (-3, 1, -1) - (2, 2, 0) t [m/s];

1.4. Z definicji prędkości średniej

t

vdt,

o

V

stąd

v =

at

T

+

bt_x

T

1.5. Przyj]

x

b

ująć oznaczenia jak na rys.4

= cos (p,

y

a

sin cp

Podnosząc oba kwadratu i dodając znaczamy tor

równania do do siebie wy-

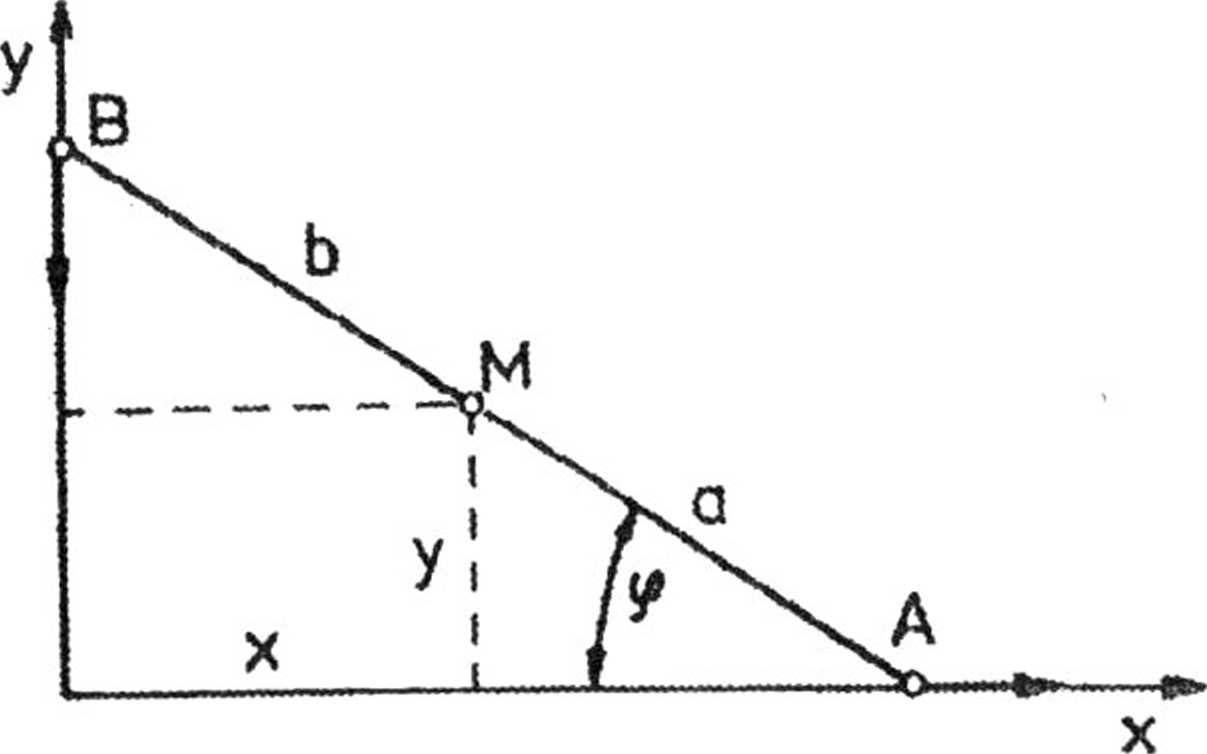
Rys.4

b²

a

i

Punkt M porusza się po elipsie o półosiach a i b

1.6. Ruch piłki określają wzory

¹ 2

2^gt’

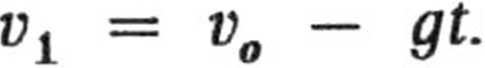
Si = vj

Z warunku

i

znajduje]

Ił

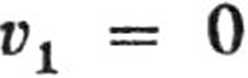
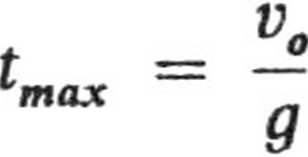
max

I